Вржащ Е.Э.
Иркутский
государственный аграрный университет им. А.А. Ежевского
Решение
уравнения диффузии при нитроцементации стали с учетом взаимодействия внедренных
элементов
Математическое описание диффузионных процессов, в том числе
многокомпонентных, обычно основано на решении уравнения диффузии (уравнения
Фика) при соответствующих краевых условиях.
Для процесса нитроцементации априори считается, что раз
диффузия насыщающих элементов осуществляется по механизму внедрения, то с
математической точки зрения можно процесс нитроцементации рассматривать как сумму двух отдельных
процессов (цементации и азотирования), т.е. решать уравнение диффузии отдельно
для углерода и азота без учета их возможного взаимодействия [1]. С другой
стороны, в этой же монографии подчеркивается, что углерод и азот оказывают друг
на друга влияние (термодинамическое, химическое и др.). Но степень этого
влияния до сих пор количественно не определялась. Поэтому было интересно
применительно к нитроцементации более общую диффузионную задачу, учитывающую
взаимодействие внедряемых элементов, и количественно определить величину этого
взаимодействия.
В этом случае надо решить систему дифференциальных
уравнений, которой коэффициент диффузии должен иметь матричную форму:
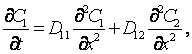
(1)

где:
С1, С2 –
концентрация соответственно углерода и азота в зависимости от глубины слоя (х)
и времени процесса (t);
D12 – коэффициент диффузии углерода под действием градиента
концентрации азота;
D21 - коэффициент диффузии азота под действием градиента
концентрации углерода;
D11 - коэффициент диффузии углерода под действием собственного
градиента концентрации;
D22 - коэффициент
диффузии азота под действием собственного градиента концентрации.
Решение системы дифференциальных уравнений (1) выполнялось
операционным, применив преобразование Лапласа-Карсона (Хевисайда) по времени t [2], при следующих
краевых условиях задачи:
C1
(x, 0) = ![]() ; C1 (0, t) =
; C1 (0, t) = ![]() ; C1 (
; C1 (![]() ) =
) =![]() ;
;
C2 (x,
0) = 0; C2 (0, t) = ![]() C2 (
C2 (![]()
при
x
![]() ,
t
,
t
![]() ,
где
,
где
![]() – исходная концентрация компонента в образце;
– исходная концентрация компонента в образце;
![]() – концентрация компонента на поверхности
раздела металл – газ
– концентрация компонента на поверхности
раздела металл – газ
(1 – углерод, 2 – азот).
Ci (x, p) = p![]() (x, t)
(x, t)![]() dt (i=1,2),
dt (i=1,2),
где
p – комплексный
параметр.
![]()
![]() p
p![]() – pC1 (x, 0) = p(
– pC1 (x, 0) = p(![]() -
- ![]() ),
),
![]() ∹ p
∹ p![]() – pC2 (x, 0) = p
– pC2 (x, 0) = p![]() .
.
Тогда решение системы уравнений (1) с учетом краевых условий
задачи будет в (x,
p) – пространстве
иметь вид:
p![]() p
p![]() + D11
+ D11![]() + D12
+ D12![]() ,
,
(2)
p![]() D21
D21![]() + D22
+ D22![]() .
.
![]() (0, p) = p
(0, p) = p![]() (0, t)
(0, t)![]() dt =
dt = ![]()
Находим частные решения системы (2) в виде
Ci = Kierx,
где r = ![]() (
3)
(
3)
Тогда, подставляя (3) в (2), получим выражение
K1D11r2erx + K2D12 r2erx = p(K1 erx - ![]() )
)
K1D21r2erx + K2D22 r2erx = pK2 erx
(4)
![]()
![]() Система
(4) будет иметь решение, отличное от нулевого, если ее определитель равен нулю,
т.е.:
Система
(4) будет иметь решение, отличное от нулевого, если ее определитель равен нулю,
т.е.:
D11r2 – p D12r2
D21r2 D22r2 - p =
0 или,
используя выражение (3),
![]()
![]() D11l2 – 1 D12l2
D11l2 – 1 D12l2
D21l2 D22l2
- 1 =
0
(5)
Раскрывая определитель (5), получим:
(D11D22
– D12D21)l4
– (D11
+ D22)l2
+ 1 = 0
(6)
![]()
![]() =
=  =
=
![]() =
= 
Значение l
будет действительным при условии l2
![]() 0, т.е. необходимыми условиями для
«действительности» l будут:
0, т.е. необходимыми условиями для
«действительности» l будут:
1) (D11 – D22)2
– 4D12D21 ![]() 0
0
2) ![]()

3) ![]()

В нашем случае необходимым условиям
п.2,3 удовлетворяют только отрицательные корни уравнения (6), т.е.
![]() l1 = -
l1 = - 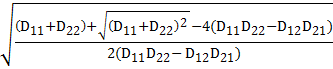
![]() l2
= -
l2
= - 
Тогда система (4) будет иметь вид
(для l1):
![]() (D11
(D11![]() – 1)
– 1)![]() +
+ ![]() D12
D12![]()
![]() = -
= - ![]()
![]() D21
D21![]() +
+ ![]() (D22
(D22![]() – 1) = 0
(7)
– 1) = 0
(7)
Система (7) имеет решение, отличное
от нулевого, если ее определитель равен нулю. Следовательно:
![]() =
-
=
- ![]()
Таким образом, частное решение
системы (1) будет иметь вид
![]() (x, p) =
(x, p) = ![]()
![]()
![]() (x, p) = -
(x, p) = - ![]()
![]()
![]() (8)
(8)
Проводя аналогичное преобразование
для l2,
получим
![]() (x, p) =
(x, p) = ![]()
![]()
![]() (x, p) = -
(x, p) = - ![]()
![]()
![]() (9)
(9)
В частных решениях (8), (9)
произвольные постоянные ![]() и
и ![]() можно положить равными единице (нормировать
их).
можно положить равными единице (нормировать
их).
Как известно из теории
дифференциальных уравнений, общее решение уравнений есть линейная комбинация
частных.
В нашем случае общее решение системы
(2) будет иметь вид:
p ![]() (x, p) = p
(x, p) = p![]() + A1
+ A1![]() (x, p) + A2
(x, p) + A2![]() (x, p)
(x, p)
p ![]() (x, p) = A1
(x, p) = A1![]() (x, p) + A2
(x, p) + A2![]() (x, p),
(x, p),
где
А1 и А2 – произвольные постоянные множители, не равные
нулю.
Используя краевые условия задачи в (x, p) – пространстве,
получаем:
A1
+ A2 = p(![]() -
- ![]()
- A1![]() – A2
– A2![]() = p
= p![]() (10)
(10)
![]()
![]() 1 1
1 1
∆ = ![]()
![]() = D21
= D21![]()
![]() , т.к.
, т.к.
![]()
![]()
![]() p(
p(![]() -
- ![]() 1
1
∆1
=
= - p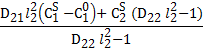
p![]() -
- ![]()
![]()
![]() 1 p(
1 p(![]() -
- ![]()
∆2
=
= - p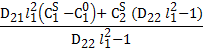
![]() p
p![]()
A1 = ![]() = - p
= - p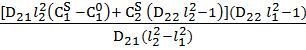
A2
= ![]() = p
= p
Итак, общее решение системы уравнений (9) будет иметь вид:
![]() (x, p) =
(x, p) = ![]() -
- 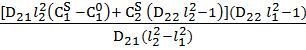
![]() +
+
+

![]()
![]() (x, p) =
(x, p) = 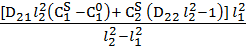
![]() -
-
- 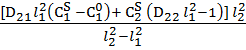
![]()
Для получения окончательного решения
необходимо перейти в исходное пространство функций – (x, t) пространство. Для этого
необходимо выполнить преобразование ![]() (x, p) ∹
Ci
(x, t) при помощи таблиц оригиналов и их
изображений [3].
(x, p) ∹
Ci
(x, t) при помощи таблиц оригиналов и их
изображений [3].
Таким образом, решение системы
уравнений (1) будет иметь вид:

(11)

где erfc η =1 - erf η и erf η = ![]() )dz – интеграл вероятности.
)dz – интеграл вероятности.
В монографии [4] на основании
формулы (11) приведена оценка диагональных и недиагональных коэффициентов
диффузии углерода и азота при нитроцементации стали в электростатическом поле и
показано, что взаимодействие внедренных элементов незначительно и для данного
технологического процесса решение уравнение диффузии может быть стандартным
[5].
Литература
1. Прженосил Б. Нитроцементация. Пер. с
чешск. «Машиностроение», Л., 1969.
2. Лаврентьев М.А., Шабат В.В. Методы теории функций
комплексного переменного. «Наука», М., 1973.
3. Диткин Б.А., Прудников А.П. Операционное исчисление.
«Высшая школа», М., 1973.
4. Вржащ Е. Высокотемпературная нитроцементация в
электростатическом поле. LAP Lambert. Düsseldorf 2017.
5. Бокштейн Б.С. Задачи по диффузии в металлах. МИСиС,
М., 1969.