Technical science /10. Mining

Associate professor Turymbetov T.A., graduate student Madenov A.N., undergraduate Aitbayev N.T.

Caspian State University of Technologies and Engineering named after

Sh. Yessenov, Aktau, Kazakhstan

The stress-strain state of underground structures in the form shtreks

In this case investigated the static elastic stress and strain state of two shallow cavities laying in heavy transtropic massif depending on the degree of discontinuity conform to small sloping layers at an angle . Let denote the depth of the workings of the distance between their centers .

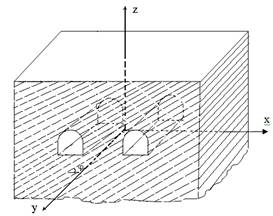
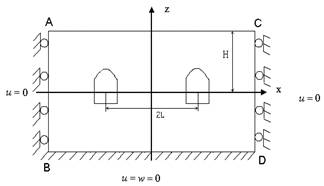
а) three dimensional view; b) two dimensional view;

Fig.1. The computational domain

Anisotropic doubly periodic massif of slits systems are replaced with solid transtropic body, equivalent stiffness basic structure, by solving the problem of reduction.

The plane of the cross-sectional areas with anisotropic in plane deformation slits; efforts are at infinity [1].

By solving the problem of bringing to an anisotropic body with the boundary conditions. Elastic parameters , transtropic solid body, equivalent stiffness anisotropic massif with slots are given [2].

Hooke's law of anisotropic massif with cavities with generalized plane strain relative to the Cartesian coordinate system (see Figure 1):

; (1)

were , , ; - deformation coefficients defined by the formulas [2].

Here - effective elastic constants transtropic massif equivalent stiffness anisotropic massif with slits, which depends on the elastic constants of the last and the geometry of the slits .

The cross-section in plane ABCD shtrek planes of deformation using units to isoparametric calculation elements (Figure 1b). Constitute the basic resolution of the system of algebraic equations finite element method’s - order relative to the projections of moving points and it can be solved with the following boundary conditions [3]:

base BD calculation area ABCD non-deformable –

; (2)

sides АВ and СD under the weight of rocks moved only in the vertical direction due to a lack of influence of cavities –

. (3)

The study estimated the area with cavities is automatically split into isoparametric elements using program FEM_3D in object-oriented environment program.

Solution of the fundamental system of equations with to finite element method’s displacement components with the boundary conditions (2), (3) rigorous methods is difficult; therefore it can be solved in an iterative method of Gauss-Seidel-relaxation factor with a given accuracy. An attractive feature of this method is as follows: firstly prepared only once and the system stiffness matrix used when iterating its elements and column elements of the matrix ; secondly, when - iteration for unknown , need values when - iteration, and for - their values for -iteration.

Applying a method of finite elements, we determine moving and as linear function [4].

Where factors is received from [5]. Now shall determine connection between and . Where and Matrix of element rigidity

(4)

Thus, the system linear algebraic equation is formed [5]:

(5)

At an angle of inclination of the plane of isotropy (and the plane of the slits) slots massif with cavities, ceteris paribus both stress and displacement are distributed symmetrically around the vertical axis and increase with the depth of emplacement of structures; reduces stress, increasing displacement with reduction w/a; when both the stress and the displacement are asymmetric about a vertical axis . When the length of the brattice 5D and more, where D-cavities of the largest diameter, interference structures is negligible.

REFERENCES

1. Erzhanov Zh.S, Aytaliev Sh.M., Masanov Zh.K. Stability of horizontal caves in the pan-layered massif. Alma-Ata, Science, 160p, 1971.

2. Erzhanov Zh.S, Kaidarov K.K., Tusupov M.T. Mountain range with a discontinuous layer coupling (plane problem). "Mechanical processes in the rock mass." Alma-Ata, "Nauka", 189p, 1969.

3. Turymbetov T., Azhikhanov N., Zhunisov N., Aimeshov Zh. Stress-strain state of two diagonal cavities weighty inclining layered massif system with slots in terms of elastic-creep deformations. - World conference on technology, innovation and entrepreneurship, pp. 2263-2271, Procedia-Social and Behavioral Sciences, Volume 195, ISSN: 1877-0428, Istanbul, Turkey, 2015.

4. Turymbetov T., Ozbay U, Massanov Zh, Aimeshov Zh. Modeling of underground

developments in anisotropic structure on the basis of the finite elements method. The 4^th International Sciences Congress "Science and Education in the Modern World"., pp.989-993, Vol. II, New Zealand, Auckland, 5-7 January, 2015.

5. Azhikhanov N., Turymbetov T., Aimeshov Zh. The shtrek well type fluid filtration simulation in the tense heterogenous layer. Yale Journal of Science and Education. Pp. 434-440. No.1. (18), Volume X, January-June, 2016.