Математика/ 5. Математичне моделювання

К. ф.-м.н. Готинчан І.З. , cт. викл. ^*Готинчан Г. І.

Чернівецький торговельно-економічний інститут

Київського національного торговельно-економічного університету

^*Чернівецький факультет Національного технічного університету

“Харківський політехнічний інститут”

Побудова розв’язку алгоритмічного характеру для задачі статики в чотирошаровому середовищі методом гібридного інтегрального перетворення типу Лежандра 2-го роду – Ганкеля 2-го роду - (конторовича - Лєбєдєва) 2-го роду – Фур’є

Останнім часом інтенсивне впровадження композитних матеріалів, при їх виготовленні та експлуатації, створює поля різної природи. Дослідження таких полів приводить до розв’язання задач математичної фізики неоднорідних середовищ, побудова розв’язків яких потребує відповідного математичного апарату. Це породило метод гібридних інтегральних перетворень (ГІП), започаткованих в працях Я.С. Уфлянда [1]. Продовження цих досліджень знаходимо в роботах В.С. Проценка [2]. Теорію ГІП закладено в працях [3, 4]. Дана робота присвячена побудові розв’язку задачі статики в неоднорідному середовищі методом ГІП.

Розглянемо задачу про побудову обмеженого в області розв’язку сепаратної системи диференціальних рівнянь Пуассона

(1)

за крайовими умовами

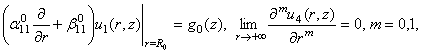(2)

(3)

і умовами спряження

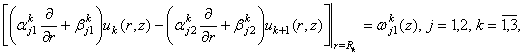(4)

де - диференціальний оператор Бесселя з виродженням в групі старших [3]: - узагальнений диференціальний оператор Лежандра [3,4]

- диференціальний оператор Бесселя з виродженням в групі молодших [3]

- диференціальний оператор Фур’є.

Запишемо систему (1) і крайові умови (3) в матричній формі:

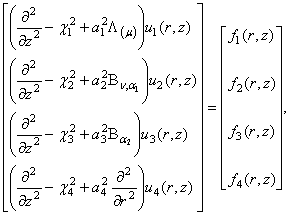(5)

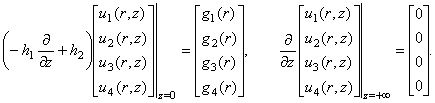(6)

Припустимо, що . Покладемо всюди Застосуємо за правилом множення матриць операторну матрицю-рядок [3] до задачі (5), (6). Внаслідок теореми про основну тотожність для оператора отримуємо лінійне диференціальне рівняння зі сталими коефіцієнтами

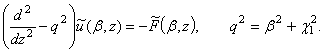(7)

Тут бере участь функція

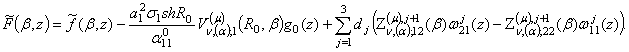
При цьому повинні справджуватися крайові умови

(8)

Розв’язком крайової задачі (7)-(8) є функція

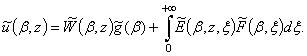(9)

У рівності (9) присутня функція Гріна

породжена крайовою умовою (8) в точці , і фундаментальна функція крайової задачі (2), (8)

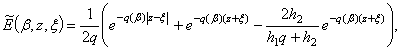
породжена неоднорідністю рівняння (7).

Застосуємо операторну матрицю-стовпець [3] за правилом мно-ження матриць до матриці-елементу де функція визначена формулою (9). Після низки елементарних перетворень отримуємо єдиний розв’язок еліптичної задачі (1) – (4):

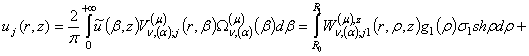
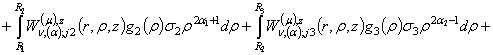
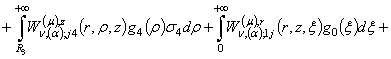(10)

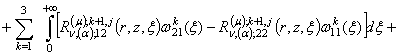
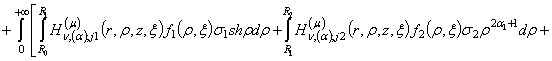
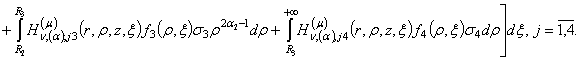
Тут беруть участь головні розв’язки даної еліптичної задачі:

1) породжені крайовою умовою на лінії функції Гріна

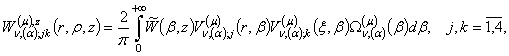
2) породжені крайовою умовою на лінії функції Гріна

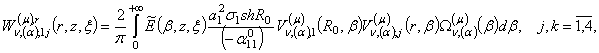
3) породжені неоднорідністю умов спряження функції Гріна

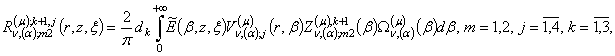
4) породжені неоднорідністю системи рівнянь (1) функції впливу

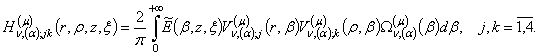
Вектор-функція , де визначені формулою (10), описує в точній аналітичній формі стаціонарний процес в даному середовищі. Алгоритмічний характер формули (10) дозволяє використовувати одержані розв’язки як в теоретичних дослідженнях, так і в інженерних розрахунках.

Література

1. Уфлянд Я.С. О некоторых новых интегральных преобразованиях и их приложений к задачам математической физики // Вопросы математической физики. – Л., 1976. – С.93-106.

2. Проценко В.С., Соловьев А.И. Некоторые гибридные интегральные преобразования и их приложения в теории упругости неоднородных сред // Прикладная механика. – 1982. – Т. ХIII, №1. – С.62-67.

3. Готинчан І.З. Гібридне інтегральне перетворення (Конторовича - Лєбєдева) – Фур’є – Бесселя – Ейлера на сегменті полярної осі/ І.З. Готинчан, Г.І. Готинчан // Математичне та комп’ютерне моделювання. Серія: Фізико – математичні науки: зб. наук. праць / Інститут кібернетики ім. В.М. Глушкова НАН України, Кам’янець – Подільський національний університет ім. І. Огієнка. - Кам’янець – Подільськ: Кам’янець – Подільський національний університет ім. І. Огієнка, 2013. – Вип. 8. – С. 33-51.

4. Готинчан І.З. Інтегральне перетворення, породжене гібридним диференціальним оператором (Конторовичча-Лєбєдєва) – Фур’є – Лежандра - Ейлера на сегменті полярної осі / І.З.Готинчан, Г.І.Готинчан // Naukowa przestrzen Europy – 2013: materialy IX miedzynarodowej naukowi – praktycznej conferencji. Volume 32. Matematyka. Fizyka. – Przemysl (07 - 15 kwietnia 2013). Nauka i studia. – P. 8-13.