Педагогические науки/2. Проблемы подготовки специалистов

К.пед.н. Сидоренко-Николашина Е.Л.

Крымский федеральный университет, Россия

Определение массы пластины с помощью двойного интеграла

Развитие рыночной экономики в России сегодня побуждает педагогов решать проблему формирования специалистов нового типа – постоянно повышающих свое профессиональное мастерство, обладающих необходимыми компетенциями и способных применить полученные в вузе теоретические знания в производственной деятельности. Повысился спрос на социально-активную личность, способную самостоятельно принимать решения и нести ответственность за их реализацию, что ведет к осознанию необходимости формирования специалистов, конкурентоспособных на рынке труда. Таким образом, компетентность, профессионализм и конкурентоспособность - это те качества специалистов, от которых зависят их трудовые и жизненные успехи.

Изучение процесса обучения студентов в высшей школе рассмотрены в работах С.И. Архангельского, В.В. Давыдова, Л.Д. Кудрявцева, В.М. Монахова, A.M. Новикова, М.Н. Скаткина и других. Способы оценки качества подготовки и совершенствования процесса формирования специалиста с социальной, экономической и педагогической точки зрения рассматриваются С.Я. Батышевым, Э.Ф. Зеером, Г.И. Ибрагимовым, А.Я. Найном, П.Н. Осиповым [3], Н.Ф. Талызиной [5], С.Н. Широбоковым и другими учеными.

Анализ теоретических и практических основ проблемы повышения качества математического образования базируется на исследованиях известных психологов, дидактов Ю.К. Бабанского, П.Я. Гальперина, А.Н. Леонтьева, А.А. Столяра [4] и др.

Все эти работы способствуют накоплению и систематизации знаний по исследуемой проблеме. Однако, остались слабоизученными такие ее аспекты как: содержание, формы и методы профессиональной подготовки конкурентоспособного инженера, определение и создание условий эффективного формирования профессиональной компетентности будущего специалиста.

Подготовка инженеров в настоящее время приобретает особую актуальность. При этом высокое профессиональное мастерство, умение самостоятельно принимать обоснованные и эффективные инженерные решения в настоящее время невозможно без овладения методами решения задач прикладного характера.

Важнейший дидактический принцип связи теории с практикой рассматривался многими учеными, например Л.В. Васяк [1], В.В. Евстигнеевым [2] и другими. Цель нашей работы – в качестве задачи практического содержания рассмотреть нахождение массы плоской фигуры (пластины), решаемую в курсе математики для студентов различных инженерных специальностей и приводящую к понятию двойного интеграла. Задачи подобного содержания представляют собой одно из приложений интегрального исчисления функции двух независимых переменных. Рассмотрение данной темы, с нашей точки зрения, следует начинать на лекции с формулировки теоретического положения и одной иллюстративной задачи, продолжить решение задач на практическом занятии.

Масса плоской пластинки D с переменной плотностью находится с помощью двойного интеграла по формуле

. (1)

Задача 1. Определить массу круглой пластины радиуса R, если поверхностная плоскость в каждой точке обратно пропорциональна расстоянию от этой точки до центра круга.

Решение. По условию имеем 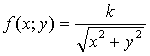, где k – коэффициент пропорциональности. По формуле (1) имеем:

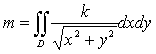. Переходя к полярным координатам, получаем

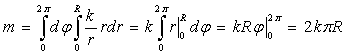(единиц массы).

Задача 2. Пластина ограничена параболой и прямой х=1. Найти массу пластины, если в каждой точке ее поверхностная плотность обратно пропорциональна расстоянию точки до директрисы параболы.

Решение. Задана парабола с вершиной в начале координат ветвью вправо. Уравнение директрисы данной параболы . Расстояние от любой точки пластинки до директрисы равно (х+1). Тогда согласно формуле (1) масса вычисляется: 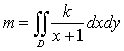, где k – коэффициент пропорциональности, а область D определяется неравенствами: . Тогда

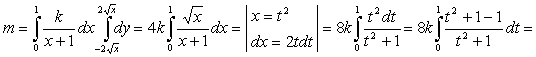
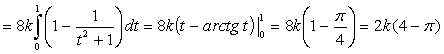(единиц массы).

Задача 3. Найти массу фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение. По формуле (1) находим массу пластины. По условию, где k – коэффициент пропорциональности.Тогда

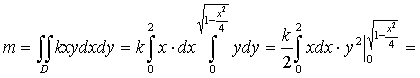
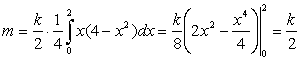(единиц массы).

Научившись решать различные задачи прикладного содержания, студенты устанавливают многогранные связи математики с физикой и дисциплинами профессионального цикла.

Анализ психолого-педагогической литературы и опыт работы в высшем учебном заведении позволяет нам сделать вывод о том, что формирование конкурентоспособности студентов является важным этапом на пути становления личности будущего специалиста, способного творчески применять свои знания на практике.

Литература:

1. Васяк Л.В. Профессионально ориентированные задачи по математике для студентов инженерных специальностей: учебное пособие [Текст] / В. А. Далингер, Л.В. Васяк. – Омск: Изд-во «Сфера», 2007. – 60 с.

2. Евстигнеев В. Интеграция фундаментального и специального знаний в подготовке инженерных кадров / В.Евстигнеев, С.Горбунов // Alma Mater (Вестник высшей школы). – 2003. – №11. – С.14-16.

3. Осипов П.Н., Суворов В.С., Как формировать конкурентоспособного специалиста: Пособие для руководителей. – Казань: ИСПО РАО, 2000. - 100 с.

4. Столяр А.А. Логические проблемы преподавания математики / А.А.Столяр. – Минск, Вышейшая школа, 1965. – 254 с.

5. Талызина Н.Ф. Управление процессом усвоения знаний (психологические основы) / Н.Ф.Талызина. – М.: Изд-во Моск. ун-та., 1984. – 346 с.