УДК
539.3
Каюмов Р.А.
– доктор физико-математических наук, профессор
E-mail: kayumov@mail.ru
Страхов Д.Е.
– кандидат технических наук, доцент
E-mail: strahov@ksaba.ru
Казанский государственный архитектурно-строительный
университет
Адрес организации: 420043, Россия, г. Казань, ул.
Зелёная, д. 1
СДВИГОВЫЕ ХАРАКТЕРИСТИКИ АРМИРОВАННЫХ ПЛАСТИКОВ
Аннотация
Разработана
методика экспериментального определения сдвиговых характеристик армированных
пластиков. Сначала построены экспериментальные зависимости напряжений от
деформаций вдоль и поперек армирования при простом растяжении стандартных
образцов. Определены механические характеристики (модули Юнга, коэффициенты
Пуассона). После этого модуль сдвига определен путем решения обратной задачи
изгиба длинных и коротких балок. Полученные характеристики проверены на
контрольных образцах.
Ключевые
слова: композитные
материалы, армированные
пластики, полимерные матрицы, сдвиговые характеристики, методы
испытания.
Современные
технологии техники и промышленности постоянно развиваются, что сказывается на
развитии новых композитных материалов. Постоянное улучшение свойств и
показателей армированных пластиков, не может не сказаться на технологиях их
испытания, подчас не удовлетворяющих возросшим механическим показателям
разрабатываемых материалов.
Одним
из таких направлений определения упругих и прочностных характеристик является
испытание на сдвиг. Следует отметить, что при нагружениях в определенных
направлениях, свойство материала в основном определяется свойствами полимерной
матрицы. Данное свойство армированных пластиков является существенным
недостатком современных перспективных материалов со слоистой и волокнистой
структурой. Следовательно, низкие сдвиговая прочность и жесткость являются
определяющими при выборе того или иного композитного материала.
Таким
образом, при постоянном росте количества новых полимерных матриц и армирующего материала необходимы технологии
правильного и простого определения сдвиговых характеристик данных композитов. Данная
проблематика рассматривалась в предыдущих работах авторов и других
исследователей [1-10].
Целью
работы являлась разработка экономичного и универсального способа определения
сдвиговых характеристик армированных пластиков.
1. При определении модуля сдвига при изгибе, рассмотрим
задачу о нагружении короткой балки (рис.1). Тогда прогиб будет происходить не
только от изгибающего момента, но и от сдвига под действием поперечной силы.
Таким образом:
, а = 0,3. (1.1)
Поскольку
, 
неизвестны, то
необходимо сформулировать математическую задачу для их определения. Для этого
нужно испытать не менее двух серий образцов с различными геометрическими
характеристиками, у которых отличаются 
и площади А. Запишем эти соотношения
для экспериментальных данных
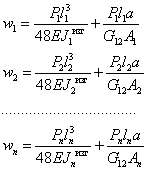(1.2)
Задача
идентификации 
формулируется следующим образом. Составим
невязку уравнений
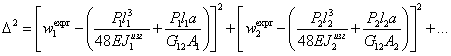(1.3)
При
известных из экспериментов значениях величин b, H, l, P, w необходимо найти 
из условия минимума невязки D2.
2. Основной трудностью в этом
подходе является то, что экспериментально определенная изгибная жесткость балки 
для композитных
материалов, как правило, меньше той, которая вычисляется с помощью модуля Юнга Е+, определенного при
растяжении этих образцов, т.е.
Это можно объяснить тем, что при сжатии
диаграмма деформирования отличается от диаграммы растяжения. В таких случаях
часто используют упрощенную модель деформирования, а именно модель разномодульного
материала с модулями Юнга Е+ и Е-. Для определения Е- целесообразно использовать эксперименты
на изгиб длинных балок. Рассмотрим задачу об изгибе балки из разномодульного
материала при центральном нагружении.
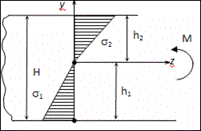
Рис.1
Примем
гипотезу плоских сечений. Тогда получим соотношение для деформаций
(2.1)
Уравнение
равновесия для части балки ∑Fz = 0 имеет вид:
Если
балка имеет прямоугольное сечение ширины b, высоты Н, то
, 
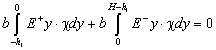(2.2)
Отсюда
вытекает уравнение
(2.3)
Связь
и h1 примет вид:
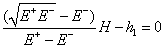(2.4)
Уравнение
для w получают обычным путем. Сначала запишем связь напряжений с изгибающим
моментом, учитывая, что балка имеет прямоугольное сечение
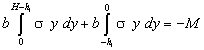(2.5)
На
основе гипотезы плоских сечений получим
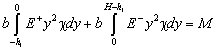(2.6)
Отсюда
следует зависимость
(2.7)
Поскольку
кривизна c при малых поворотах представляет собой вторую производную
прогиба w, то получим уравнение в виде
(2.8)
где
– изгибная жесткость
балки:
(2.9)
В
нашем случае решение уравнения (2.8) известно и выражение для
экспериментального значения изгибной жесткости 
примет вид:
(2.11)
Тогда формула для определения 
примет вид:
(2.10)
После
этого можно вычислять 
для любых
размеров балок и подставлять в
выражение для 
.
3.
Приведем данные некоторых экспериментов и результаты их обработки. При
испытании на изгиб пултрузионных стеклопластиков образцы изготавливались путем
вырезания из плиты с размерами 300х400х10 (мм) вдоль армирования. После
изготовления образцы выдерживались не менее суток при температуре 24 градуса и
влажности 45%. Испытания проводились (см. рис. 2) при температуре 24 градуса и
влажности 45%.
После измерения размеров осуществлялось жесткое
нагружение вплоть до разрушения (см. рис. 3) с пошаговым измерением нагрузки и прогиба. Диаграммы
деформирования при изгибе для угла укладки 0о см. на рис.4,5. Таблицы
определения механических характеристик см. табл. 1-4.
Рис.2.
Испытание пултрузионного стеклопластика
Рис.3.
Образцы пултрузионного стеклопластика с армированием 0° после разрушения при
изгибе
2 3 4 1
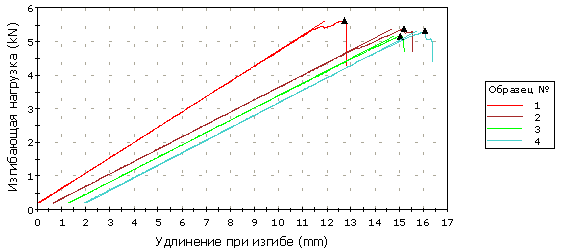
Рис.4. Диаграммы деформирования при изгибе поперек плоскости
образца при угле укладки 0о
5 4 3 2 1
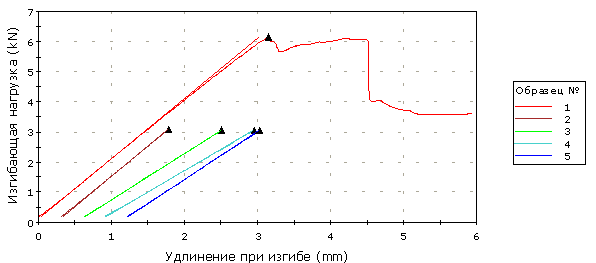
Рис.5. Диаграммы
деформирования при изгибе в плоскости образца при угле укладки 0º
Испытание образцов на
изгиб поперек плоскости образца, 0°
Таблица 1.
|
№ |
Расстояние между опорами (мм) |
Толщина (мм) |
Ширина (мм) |
Максимальная изгибающая нагрузка Р (кН) |
Изгибный модуль Юнга (ГПа) |
Прогиб при максимуме нагрузки (мм) |
Деформация при максимальной изгибающей
нагрузке |
Напряжение при максимуме нагрузке (МПа) |
|
1.1 |
170,0 |
9,8 |
23,1 |
5,614 |
25,85 |
12,7187 |
0,02588 |
645,262 |
|
1.2 |
170,0 |
9,8 |
20,4 |
5,373 |
23,58 |
14,5427 |
0,02959 |
699,348 |
|
1.3 |
170,0 |
9,8 |
20,1 |
5,169 |
23,95 |
13,7596 |
0,02800 |
682,823 |
|
1.4 |
170,0 |
9,8 |
20,5 |
5,3169 |
23,73 |
14,147 |
0,02878 |
688,644 |
|
Максимум |
|
|
|
5,61 |
25,85 |
14,543 |
0,030 |
699,35 |
|
Минимум |
|
|
|
5,17 |
23,58 |
12,719 |
0,026 |
645,26 |
|
Среднее |
|
|
|
5,37 |
24,28 |
13,792 |
0,028 |
679,02 |
|
Диапазон |
|
|
|
0,45 |
2,27 |
1,824 |
0,004 |
54,09 |
|
Коэф. вар. |
|
|
|
3,45 |
4,36 |
5,682 |
5,677 |
3,46 |
|
Стандарт. отклонение |
|
|
|
0,19 |
1,06 |
0,784 |
0,002 |
23,52 |
Испытание коротких образцов на изгиб
в плоскости образца
Таблица 2.
|
№ |
Расстояние между опорами (мм) |
Толщина (мм) |
Ширина (мм) |
Изгибающая максимальная нагрузка (кН) |
Модуль Юнга (ГПа) |
|
1.3 |
80,00 |
24,30 |
9,80 |
4,39795 |
7,84805 |
|
1.8 |
80,00 |
20,85 |
9,80 |
3,07000 |
9,46986 |
|
1.9 |
80,00 |
21,43 |
9,80 |
3,06382 |
9,23293 |
|
1.10 |
80,00 |
20,60 |
9,80 |
3,11209 |
10,42970 |
|
1.11 |
80,00 |
21,00 |
9,80 |
3,03831 |
10,45063 |
Испытание коротких образцов
на изгиб в плоскости образца Таблица
3.
|
№ |
Прогиб при максимуме нагрузки (мм) |
Напряжение при максимуме изгибающей нагрузки (МПа) |
|
1.3 |
0,5815 |
91,19961 |
|
1.8 |
0,4747 |
86,47325 |
|
1.9 |
0,5097 |
81,69111 |
|
1.10 |
0,4538 |
89,79942 |
|
1.11 |
0,4189 |
84,36236 |
|
Максимум |
0,5815 |
91,1996 |
|
Минимум |
0,4189 |
81,6911 |
|
Среднее |
0,48772 |
86,7052 |
|
Диапазон |
0,1626 |
9,5085 |
|
Коэф. вар. |
12,6949 |
4,48385 |
|
Стандарт. отклонение |
0,0619154 |
3,88773 |
Испытание образцов на
изгиб в плоскости образца Таблица 4.
|
№ |
Расстояние между опорами (мм) |
Толщина (мм) |
Ширина (мм) |
Изгибающая максимальная нагрузка (кН) |
Модуль Юнга (ГПа) |
Прогиб при максимуме нагрузки (мм) |
Напряжение при максимуме изгибающей нагрузки (МПа) |
|
1.1 |
170,0 |
22,9 |
9,8 |
6,1508 |
20,829 |
3,153 |
305,193 |
|
1.2 |
170,0 |
23,1 |
9,8 |
3,0844 |
20,497 |
1,486 |
150,403 |
|
1.3 |
170,0 |
20,4 |
9,8 |
3,0591 |
22,695 |
1,921 |
191,269 |
|
1.4 |
170,0 |
20,1 |
9,8 |
3,0482 |
21,86 |
2,063 |
196,319 |
|
1.5 |
170,0 |
20,5 |
9,8 |
3,046 |
23,131 |
1,852 |
188,596 |
|
Максимум |
|
|
|
6,151 |
23,131 |
3,153 |
305,193 |
|
Минимум |
|
|
|
3,046 |
20,497 |
1,486 |
150,403 |
|
Среднее |
|
|
|
3,678 |
21,802 |
2,095 |
206,356 |
|
Диапазон |
|
|
|
3,105 |
2,634 |
1,667 |
154,790 |
|
Коэф. вар. |
|
|
|
37,594 |
5,238 |
30,005 |
28,198 |
|
Стандарт. отклонение |
|
|
|
1,383 |
1,142 |
0,629 |
58,188 |
В результате обработки
результатов экспериментов на изгиб в плоскости балок получены следующие характеристики материала
Е+ =
30 ГПа, Е- = 18,894 ГПа, G12 = 1, 445 ГПа.
Для проверки правильности
определения Е- были использованы эксперименты на изгиб балок поперек их плоскости.
Были вычислены их прогибы с использованием уже найденных
модулей Юнга при растяжении и сжатии. Расчетные значения w
отличались от
экспериментальных на величины не более 4%, что говорит о применимости модели разномодульного материала для определения
модуля сдвига из экспериментов на изгиб
длинных и коротких балок.
СПИСОК
ЛИТЕРАТУРЫ
1.
Гребенюк
С.Н. Модуль сдвига волокнистого композита с трансверсальноизотропными матрицей
и волокном. Прикладная математика и механика. 2014. Т.78. №2. С.270-276.
2.
Янкин А.С.,
Словиков С.В., Бульбович Р.В. Определение динамических механических свойств
низкомолекулярных вязкоупругих композитов при бигармоническом законе нагружения.
Механика композиционных материалов и конструкций. 2013. Т.19. №1. С.141-151.
3.
Лурье С.А.,
Соляев Ю.О., Андрюнина М.А., Лыскова Е.Д. Оптимизация демпфирующих
характеристик слоистых композитных материалов, содержащих волокна с
вязкоупругим покрытием. Вестник Пермского национального исследовательского
политехнического университета. Механика. 2012. №3. С.98-119.
4.
Каюмов Р.А.
Расширенная задача идентификации механических характеристик материалов по
результатам испытаний конструкций из них // Известия РАН. Механика твердого
тела.- 2004.- № 2. – С.94-103.
5.
Закиров
И.М., Алексеев К.А., Каюмов Р.А., Гайнутдинов И.Р. Пути повышения прочностных
характеристик складчатых заполнителей, выполненных из листовых композиционных
материалов. //Авиационная техника, №3
2009г. 5стр.
6.
Воронцов Г.
В., Плющев Б. И., Резниченко А. И. Определение
приведенных упругих характеристик армированных
композитных материалов методами
обратных задач тензометрирования // Мех. композ. мат.,
1990. № 4. с.733-747.
7.
Каюмов Р.А.
Связанная задача расчета механических характеристик материалов и конструкций из
них // Известия РАН. Механика твердого тела.- 1999.- № 6. - С.118-127.
8.
Терегулов
И..Г., Каюмов Р.А., Бутенко Ю.И., Сафиуллин Д.Х. Определение механических
характеристик композитов по результатам испытаний многослойных образцов // Механика композитных материалов. Рига. -
1995.- Т.31, № 5. - С.607 - 615.
9.
Суворова
Ю.В., Добрынин В.С., Статников И.Н., Барт Ю.Я. [1]. Определение свойств
композита в конструкции
методом параметрической идентификации // Мех. композ.
мат., 1989. № 1.
с.150-157.
10.
Алфутов
Н.А., Зиновьев П.А., Попов Б.Г. Расчет
многослойных пластин и оболочек из композиционных материалов. - М.:
Машиностроение, 1984. 263с.
Kayumov R.A. –
doctor of physical and mathematical sciences, professor
E-mail: kayumov@mail.ru
Strahov D.E. – candidate
of technical scinces, associate professor
E-mail: strahov@ksaba.ru
Shakirzyanov F.R. – candidate
of physical and mathematical sciences, senior lecturer
E-mail: faritbox@mail.ru
Kazan State
University of Architecture and Engineering
The organization address: 420043, Russia, Kazan, Zelenaya st., 1
DETERMINATION OF
SHEAR PERFORMANCE OF REINFORCED PLASTICS
Resume
The technique of experimental
determination of shear performance of reinforced plastics. First constructed
experimental stress-strain along and across the reinforcement in simple tension
of standard samples. Defined mechanical properties (Young's modulus, Poisson's
ratio). After that, the shear modulus is determined by solving the inverse
problem of the bending of long and short beams. The characteristics obtained
for the control samples tested.
Keywords: composite
materials, reinforced plastics, polymer matrix, the shear characteristics,
testing methods.
References
1.
Grebenyuk S. The shear modulus of the fibrous
composite transversalnoizotropnymi matrix and fiber. Applied Mathematics and Mechanics. 2014.
T.78. №2. S.270-276.
2.
Yankin AS,
Slovic SV, RV Bulbovich Determination of dynamic mechanical properties of low
molecular weight viscoelastic composites at Biharmonic law loading. Mechanics of composite materials and
structures. 2013. T.19. №1. S.141-151.
3.
Lurie SA, Sol
JO, Andryunin MA Liskova ED Optimization of the damping characteristics of the
layered composite material comprising fibers coated with a viscoelastic. Bulletin of Perm National Research
Polytechnic University. Mechanics. 2012. №3. S.98-119.
4.
RA Kayumov
Extended problem of identification of mechanical properties of materials based
on the results of these test structures // Proceedings of the Academy of
Sciences. Mechanics of rigid
body, 2004.- № 2. - S.94-103.
5.
IM Zakirov, Alexeev KA, RA Kayumov, Gainutdinov IR
Ways to improve the strength characteristics of folded fillers made of
composite sheet materials. // Aviation equipment, №3, 2009. 5str.
6.
GV Vorontsov, ivy BI, Reznichenko AI definitions of
the elastic characteristics of reinforced composite materials by means of
inverse problems of strain measurement // Mech. Composite. Math., 1990. № 4. s.733-747.
7.
Kayumov RA A related problem of calculating the
mechanical properties of materials and structures are // Izvestiya RAN. Mechanics of rigid body, 1999.- № 6. -
S.118-127.
8.
Teregulov I..G., RA Kayumov, Yu Butenko, Safiullin DH
Determination of mechanical properties of composites based on the results of
tests of multilayer samples // Mechanics of Composite Materials. Riga. - 1995.- T.31, № 5. - S.607 - 615.
9.
9. Y.
Suvorov, Dobrynin VS Statnikov IN, Bart YY. Defining the properties of the
composite construction method of parametric identification // Mech. Composite.
Math., 1989. № 1. s.150-157.
10. Alfutov
NA Zinoviev PA, Popov BG Calculation of laminated plates and shells made of
composite materials. - M .: Engineering, 1984. 263s.