Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

расчет точек пересечения двух параметров

В представленной ниже статье рассмотрен вопрос влияния трех переменных на два параметра V1 и V2, а также расчет точек пересечения этих параметров. При этом переменные являются постоянными и увеличиваются. То есть, в предлагаемой статье рассмотрена зависимость изменения V1 (V2) = f(Х1, Х2, Х3).

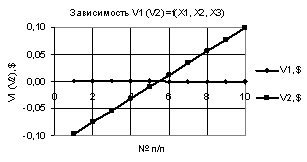
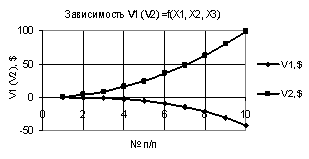
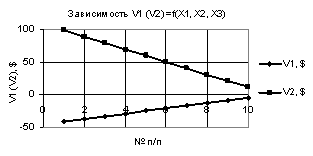
На первом рис. 1 показаны две зависимости V1 и V2 при Х1 = 1…-1, Х2 = Х3 = -0,01. Из данного рисунка видно, что значения V2 увеличиваются со значения -0,1 до своей максимальной величины V2 = 0,1, т.е. в 1,014 раза. Параметр V1 при данном масштабе представляет собой практически прямую, параллельную оси Х, хотя на самом деле он имеет наклонный, уменьшаясь слева на право.

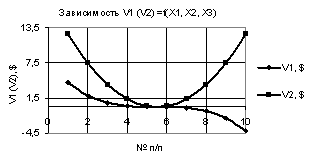
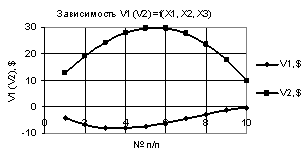
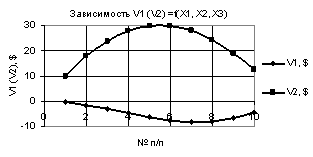
Рис. 1. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 = Х3 = -0,01	Рис. 2. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 = Х3 = 0,99…-0,99
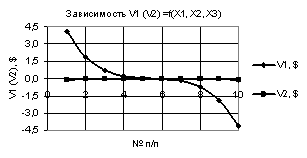
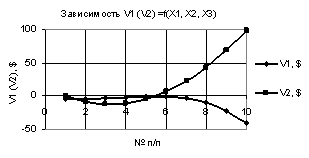
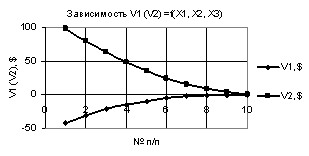
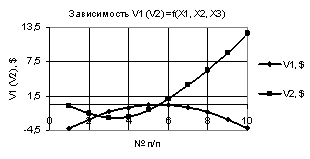
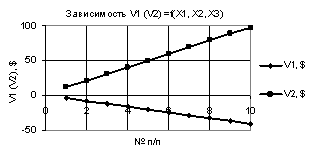
Рис. 3. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 = Х3 = -0,99…0,99	Рис. 4. V1 (V2) = f(X1, Х2, Х3) при Х1 = -1, Х2 = Х3 = 0,99…-0,99

Следующий рис. 2 дает наглядное представление, что при значениях переменных Х1 = 1…-1, Х2 = Х3 = 0,99…-0,99 построенные две кривые V1 и V2 приближаются друг к другу, но не соединяются. Так, например, их минимальные значения следующие V1 = 0,01 и V2 = 0,015 соответственно.

На следующих двух рисунках 3 и 4 показаны две зависимости V1 и V2, которые пересекаются. На рис. 3 зависимости V1 и V2 пересекаются между 5 и 6 точками, а на рис. 4 построенные кривые V1 и V2 имеют две точки пересечения, между точками 2 и 3, а также между точками 5 и 6 соответственно.

Рис. 5. V1 (V2) = f(X1, Х2, Х3) при Х1 = -1…-10, Х2 = Х3 = -0,99…-0,99		Рис. 6. V1 (V2) = f(X1, Х2, Х3) при Х1 = -1…-10, Х2 = Х3 = -0,99…-0,09
Рис. 7. V1 (V2) = f(X1, Х2, Х3) при Х1 = -1…-10, Х2 = Х3 = 0,99…-0,99	Рис. 8. V1 (V2) = f(X1, Х2, Х3) при Х1 = -1…-10, Х2 =Х3 = -0,99

Следующие два рисунка 5 и 6 были построены при Х1 = -1…-10, Х2 = Х3= -0,99…-0,99 и Х1 = -1…-10, Х2 = Х3 = -0,99…-0,09. Из рисунков видно, что изображенные две кривые V1 и V2 не имеют точек пересечения в рассматриваемом диапазоне масштаба.

Для построения двух 2D графиков на рисунках 7 и 8 были использованы следующие значениях переменных Х1 = -1…-10, Х2 = Х3 = 0,99…-0,99 и Х1 = -1…-10, Х2 = Х3 = -0,99. Здесь на рис. 7 представленные кривые V1 и V2 имеют две точки пересечения, которые находятся между точками 1 и 2, а также точками 5 и 6. На рис. 8 представленные расходящиеся зависимости V1 и V2 имеют линейной вид и не пересекаются между собой при данных переменных.

Построенные две сходящиеся зависимости V1 и V2 на рис. 9 при Х1 = -10…-1, Х2 = Х3 = -0,99 также представляют собой линейный вид и не имеют точки пересечения.

Из следующего рис. 10 видно, что кривые V1 и V2 при переменных Х1 = -10…-1, Х2 = Х3 = -0,09…-0,99 не имеют точек пересечения и при этом имеют максимум для кривой V1 и минимум для кривой V2.

Рис. 9. V1 (V2) = f(X1, Х2, Х3) при Х1 = -10…-1, Х2 = Х3 = -0,99

Рис. 10. V1 (V2) = f(X1, Х2, Х3) при Х1 = -10…-1, Х2 = Х3 = -0,09…-0,99

Рис. 11. V1 (V2) = f(X1, Х2. Х3)

при Х1 = -10…-1, Х2 = Х3 = -0,99…-0,09

На последнем рисунке 11 были построены две кривые V1 и V2 при Х1 = -10…-1, Х2 = Х3 = -0,99…-0,09. Здесь на представленном рисунке построенные зависимости сближаются и не имеют точки пересечения.