Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

определение точек пересечения двух кривых при разных переменных

В представленной ниже статье рассмотрен вопрос влияния трех переменных на два параметра V1 и V2, а также расчет точек пересечения этих параметров. При этом переменные являются постоянными и увеличиваются. То есть, в предлагаемой статье рассмотрена зависимость изменения V1 (V2) = f(Х1, Х2, Х3).

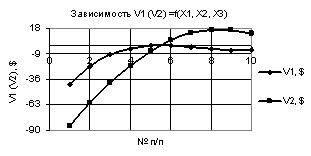
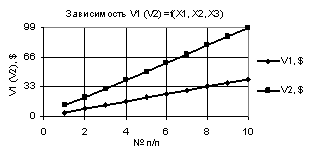
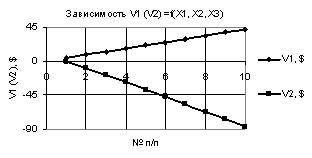
На рис. 1 показаны две зависимости V1 и V2 при Х1 = -10…-1, Х2 = Х3 = 0,99…-0,99. Из этого рисунка видно, что построенные зависимости V1 и V2 имеют одну точку пересечения, которая находится между 5 и 6 точками. При этом кривая V1 имеет минимум -4,97 в точке 9, а V2 максимум 16,52 в точке 8.

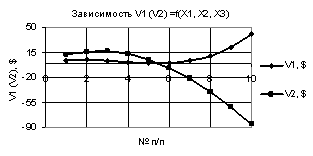
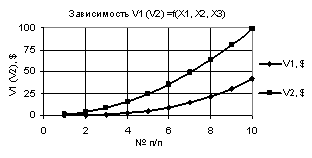
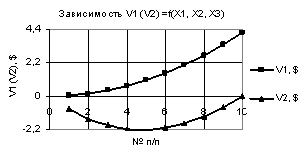
Рис. 1. V1 (V2) = f(X1, Х2. Х3) при Х1 = -10…-1, Х2 = Х3 = 0,99…-0,99	Рис. 2. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…10, Х2 = Х3 = 0,99…-0,99
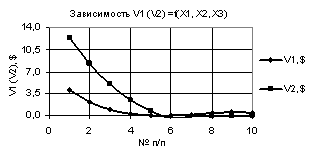
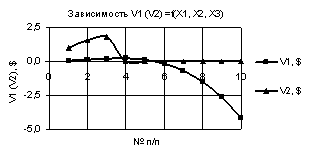
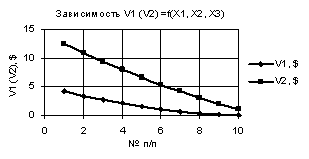
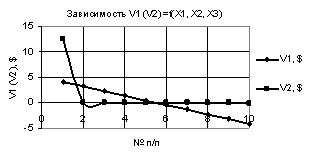
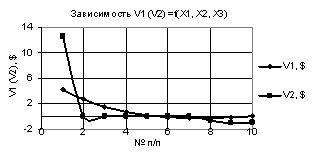
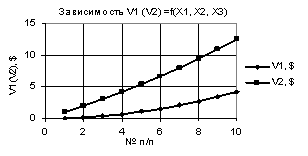
Рис. 3. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…0.1, Х2 = Х3 = 0,99…-0,99	Рис. 4. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 = Х3 = 0,99

Следующий рис. 2 дает наглядное представление, что при значениях переменных Х1 = 1…10, Х2 = Х3 = 0,99…-0,99 построенные две кривые V1 и V2 также пересекаются между точками 5 и 6. Здесь кривая V1 имеет минимальное значение 0,15 в точке 5, а кривая V2имеет максимум 16,52 в точке 3.

На следующих двух рисунках 3 и 4 показаны две зависимости V1 и V2, которые пересекаются. На рис. 3 зависимости V1 и V2 пересекаются между 5 и 6 точками, а на рис. 4 построенные кривые V1 и V2 имеют две точки пересечения, между точками 2 и 3, а также между точками 5 и 6 соответственно. Кроме того они имеют минимумы 0,025 и -0,4 в точках 5 соответственно.

Рис. 5. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…10, Х2 = Х3 = 0,99		Рис. 6. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…10, Х2 = Х3 = 0.1…0.99
Рис. 7. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 =Х3= 0.1…0.99	Рис. 8. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…-1, Х2 = Х3 = 0.99…0.1

Следующие два рисунка 5 и 6 были построены при Х1 = 1…10, Х2 = Х3 = 0,99 и Х1 = 1…10, Х2 = Х3 = 0.1…0.99. Из данных рисунков видно, что изображенные кривые V1 и V2 не имеют точек пересечения в рассматриваемом диапазоне масштаба.

Для построения двух графиков, представленных на рисунках 7 и 8 были использованы следующие значениях переменных Х1 = 1…-1, Х2 = Х3 = 0.1…0.99 и Х1 = 1…-1, Х2 = Х3 = 0.99…0.1. Здесь на рис. 7 представленные кривые V1 и V2 имеют две точки пересечения, которые находятся между точками 3 и 4. На рис. 8 представленные кривые V1 и V2 имеют одну точку пересечения между точками 1 и 2.

Построенные две сходящиеся зависимости V1 и V2 на рис. 9 при Х1 = 1…10, Х2 = Х3 = -0.99 представляют собой линейный вид и не имеют точки пересечения.

Из следующего рис. 10 видно, что кривые V1 и V2 при переменных Х1 = 1, Х2 = Х3 = -0.1…-0.99 и у них нет точек пересечения, но при этом кривая V2 имеет минимум -2,23 в точке 5.

Рис. 9. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1…10, Х2 = Х3 = -0.99		Рис. 10. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1, Х2 = Х3 = -0.1…-0.99
Рис. 11. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1, Х2 = Х3 = 0.99…0.1	Рис. 12. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1, Х2 = Х3 = 0.1…0.99

На последних двух рисунках 11 и 12 были построены две кривые V1 и V2 при Х1 = 1, Х2 = Х3 = 0.99…0.1 и Х1 = 1, Х2 = Х3 = 0.1…0.99. Здесь на рис. 11 построенные зависимости сближаются, а на рис. 12 расходятся и в обоих случаях они не имеют точки пересечения.

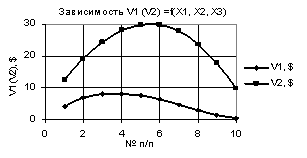
Рис. 13. V1 (V2) = f(X1, Х2, Х3) при Х1 = 1, Х2 = Х3 = 0.99…0.1

На рис. 13 кривые V1 и V2 имеют максимумы в точках 4 и 5 соответственно.