Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

Выявления функции влияния одно парамЕТРА на другой

В представленной ниже статье рассмотрен вопрос выявления влияния одного параметра V1 на другой параметр V2. При этом три переменные, на основе которых рассчитывались данные параметры, были как постоянные, так и увеличивались. То есть, в предлагаемой статье рассмотрена зависимость изменения V2 = f(V1).

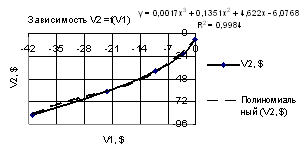
На рис. 1 показана зависимость V2 = f(V1) при Х1 = 1…-1, Х2 = Х3 = -0,01. Из этого рисунка видно, что построенную зависимость можно прогнозировать с использованием полиномиальной зависимости третьей степени с высокой точностью, т.к., здесь коэффициент корреляции R² = 0.9984.

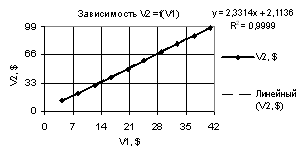
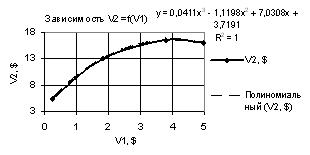
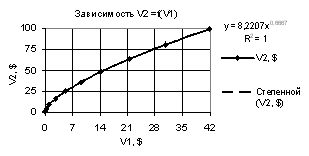
Рис. 1. Зависимость V2 = f(V1) при Х1 = -10…-1, Х2 = Х3 = 0,99…-0,09	Рис. 2. Зависимость V2 = f(V1) при Х1 = 1…10, Х2 = Х3 = 0,99…-0,99
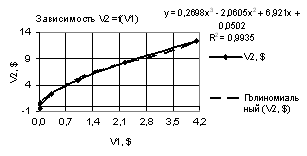
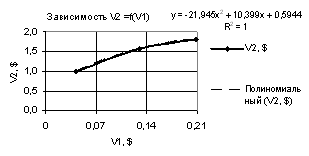
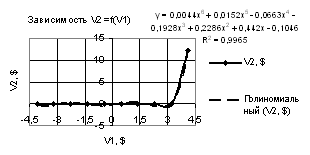
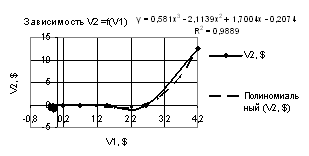
Рис. 3. Зависимость V2 = f(V1) при Х1 = 1…0.1, Х2 = Х3 = 0,99…-0,99	Рис. 4. Зависимость V2 = f(V1) при Х1 = 1…-1, Х2 = Х3 = 0.99

Следующий рис. 2 показывает как изменяется параметр V1 от переменной V2. Здесь зависимость V2 = f(V1) была построена при Х1 = 1…-1, Х2 = Х3 = 0,99…-0,99. Ее прогноз можно осуществить с помощью полиномиальной зависимости третьей степени, у которой получился следующий коэффициент корреляции R² = 1.

На следующих двух рисунках 3 и 4 показаны две зависимости V2 = f(V1) при Х1 = 1…-1, Х2 = Х3 = -0,99…0,99 и Х1 = -1, Х2 = Х3 = 0.99…-0.99 соответственно. В этих примерах в обоих случаях следует при прогнозе применять полиномиальной зависимости третьей и шестой степеней, у которых получились следующие коэффициенты корреляции R² = 0.9935 и R² = 0.9965 соответственно.

Рис. 5. Зависимость V2 = f(V1) при Х1 = -1…10, Х2 = Х3 = 0.99		Рис. 6. Зависимость V2 = f(V1) при Х1 = 1…10, Х2 = Х3 = 0.1…0.99
Рис. 7. Зависимость V2 = f(V1) при Х1 = 1…-1, Х2 =Х3= 0.09…0.99	Рис. 8. Зависимость V2 = f(V1) при Х1 = 1…-1, Х2 = Х3 = 0.99…0.09

Следующие два рисунка 5 и 6 были построены при Х1 = -1…-10, Х2 = Х3 = -0.09…-0.99 и Х1 = 1…10, Х2 = Х3 = -0.99…-0.09. Из рисунка 5 видно, что значения V2 можно прогнозировать с использованием линейной функции, которой коэффициент корреляции R² = 0.999. Значения же V2 для рис. 6 можно прогнозировать с использованием степенной функции с коэффициентом корреляции R² = 1.

Для построения двух графиков, представленных на рисунках 7 и 8 были использованы следующие значениях переменных Х1 = -1…-10, Х2 =Х3= 0.99…-0.09 и Х1 = -1…-10, Х2 = Х3 = -0.99. Здесь при прогнозе параметра V2 следует применять полиномиальные зависимости второй и третьей степеней, у которых получились следующие коэффициенты корреляции R² = 1 и R² = 0,9889 соответственно

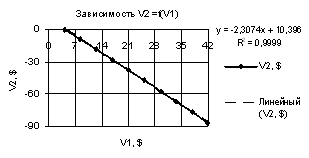
Построенная зависимость V2 на рис. 9 при Х1 = -10…-1, Х2 = Х3 = -0.99 представляют собой прямую и поэтому следует при ее прогнозе использовать линейную функцию с коэффициентом корреляции R² = 0.9999.

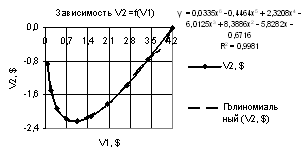
Из следующего рис. 10 видно, что при прогнозе кривой V2, построенной при переменных Х1 = -10…-1, Х2 = Х3 = -0.09…-0.99, следует применять полиномиальную зависимость шестой степеней, у которой коэффициент корреляции R² = 0.9961.

Рис. 9. Зависимость V2 = f(V1) при Х1 = -10…-1, Х2 = Х3 = -0.99

Рис. 10. Зависимость V2 = f(V1) при Х1 = -10…-1, Х2 = Х3 = -0.09…-0.99

Рис. 11. Зависимость V2 = f(V1)

при Х1 = -10…-1, Х2 = Х3 = -0.99…-0.09

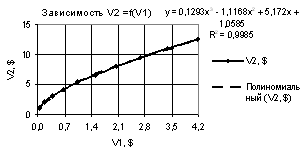
На последнем рисунке 11 представлена кривая V2 при Х1 = -10…-1, Х2 = Х3 = -0.99…-0.09. В этом примере при прогнозе следует применять полиномиальную зависимость третей степеней, у которой коэффициент корреляции R² = 0.9985.