Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

ДВНЗ “Прикарпатський національний університет імені Василя Стефаника”

Комбіновані методи наближеного розв’язання задачі Коші для квазілінійного рівняння з частинними похідними першого порядку

Розглянемо задачу Коші для квазілінійного диференціального рівняння з частинними похідними першого порядку            

(1)

(2)

де .

Означення 1 Обмежена вимірна функція називається узагальненим розв’язком задачі (1),(2), якщо

виконується нерівність

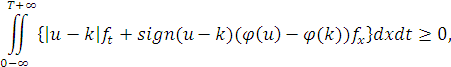
а початкова умова (2) приймається у сильному сенсі.

Зауважимо, що результати існування та єдиності розв’язку задачі (1),(2) були отримані починаючи з 1950-х років в працях Олійник О. А., Кружкова С. М. та Lax P. Водночас викликає інтерес питання отримання розв’язків з допомогою конструктивних методів побудови наближених розв’язків. У працях [1],[2],[3] було розглянуто як конкретні методи, так і загальний підхід, який дозволяє обґрунтовувати збіжність разом з отриманням оцінок швидкості в наближених методах. У праці [4] розглянуто наближений метод з використанням методу в’язкості та методу згладжування. У даній роботі ми узагальнюємо цей підхід і розглядаємо апроксимації задачі (1), (2), які будуються на основі одночасного застосування довільних наближених методів.

Нехай і при , – наближений розв’язок за методом задачі Коші (1), (2), запропонований в [1].

Далі, нехай при , наближений розв’язок за методом задачі Коші (1), (2), запропонований в [1].

Отримано оцінки збіжності наближених розв’язків до узагальненого розв’язку задачі (1),(2) у наступному сенсі.

Означення 2 При функція , яка на різних смугах є почерговим наближеним розв’язком за методом і за методом , називається наближеним розв’язком задачі (1),(2).

Теорема 1 Нехай  . Тоді для наближеного розв’язку при справджується оцінка

де функція залежить від модуля неперервності в початкової функції та від швидкості збіжності в наближених методах і

Теорема 2 Нехай . Тоді для наближеного розв’язку при справджується оцінка

,

де залежить від від швидкості збіжності в наближених методах і

Теорема 3 Нехай  . Тоді для наближених розв’язків і , і таких, що відповідають початковим функціям та справджується оцінка

де функція залежить від сумісного модуля неперервності в початкових функції та та від швидкості збіжності в наближених методах і

Теорема 4 Нехай і Тоді для наближених розв’язків і при і таких, що відповідають початковим функціям та справджується оцінка

де залежить від від швидкості збіжності в наближених методах і

Доведення теорем аналогічне до доведення тверджень в [1,2] і ґрунтується на оцінці функціонала

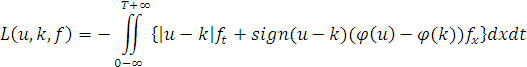
із застосуванням оцінок для модулів неперервності в наближених розв’язків, які дозволять отримати компактність сім’ї наближених розв’язків.

Зауважимо, що варіація розмірів смуг, на яких почергово застосовуються наближений метод та наближений метод , дозволяє оптимізувати швидкість збіжності наближених розв’язків до точного.

Зрозуміло, що із теорем 1-4 незалежно можна отримати існування та, що надзвичайно важливо, єдиність узагальненого розв’язку задачі (1),(2).

Література:

1.Казмерчук А. И. О сходимости приближённых решений задачи для квазилинейных уравнений первого порядка. - Вестник МГУ. - Сер. матем. механ.,-1989.-Вып.4,с.68-70

2.Казмерчук А.І. До обґрунтування наближених методів розв’язання квазілінійних законів збереження з негладкими даними задачі. - Вісник національного університету “Львівська політехніка”, Прикладна математика.-2000.-№411.-с.147-151

3. Казмерчук А. І. Наближення параболічними системами рівнянь вищих порядків систем квазілінійних диференціальних рівнянь з частинними похідними першого порядку, - “Veda a vznik – 2016”.-D.10.-S.95-97. Розміщена: Проблемы научной мысли.-Т.12-№10-2016-с.095-097.

4. Казмерчук А. І. В’язкісно-згладжувальний метод розв’язання задачі Коші для квазілінійного рівняння з частинними похідними першого порядку, - “Veda a vznik – 2016”.-D.10.-S.98-100. Розміщена: Проблемы научной мысли.-Т.12-№10-2016-с.098-100.