Вржащ Е.Э.

Иркутский государственный аграрный университет им. А.А. Ежевского

Каноническая форма математической модели процесса нитроцементации в электростатическом поле

Методы математического планирования эксперимента позволяют достаточно эффективно и быстро определять параметры многофакторных технологических процессов. Таким является процесс нитроцементации (насыщения металлических деталей углеродом и азотом из газовой среды) в электростатическом поле (ЭП), оптимизация параметров которого проводилась при помощи математических методов [1- 4].

Исследования показали, что нитроцементацию в ЭП можно удовлетворительно описать не только линейной, но и нелинейной моделью, каноническая форма уравнения которой позволяет построить ее геометрический образ [5]. Существует несколько способов описания поверхности отклика [6]. В случае, когда центр эксперимента находится вблизи экстремальной точки поверхности отклика, наиболее целесообразным является построение некомпозиционного плана второго порядка.

Проведенные исследования и расчеты показали [5], что "почти стационарная" область при нитроцементации в ЭП будет описываться нелинейным уравнением:

y = d = 0,67 + 0,14x₁ – 0,06x₂ – 0,07x₅ – 0,14 – 0,04 – 0,10 – 0,08x₂x₅, (1)

где у (d) – комплексный параметр оптимизации (функция «желательности»), х_i -параметры оптимизации.

Уравнение (1) является адекватным при 5%-уровне значимости.

Для более полной интерпретации полученных данных уравнение (1) необходимо упростить, привести к канонической форме.

Каноническое преобразование квадратичного уравнения заключается в выборе новой системы координат, в которой уравнение принимает наиболее простой вид. Такого рода преобразование сводится к параллельному переносу начала координат в новый центр и к повороту координатных осей вокруг этого центра. При этом в исходном уравнении исчезают линейные члены и члены, содержащие парные взаимодействия. Для избавления от линейных членов уравнение дифференцируется по каждой из независимых переменных и частные производные приравниваются нулю.

В нашем случае:

= 0,14 – 0,28x₁ = 0

= - 0,06 – 0,08x₅ = 0

= - 0,07 – 0,20x₅ – 0,08x₂ = 0.

Решим эту систему с помощью определителей:

0,28 0 0

∆ = 0 -0,08 -0,08 = 0,002688 (∆ поверхность отклика имеет

0 -0,08 -0,20 центр);

0,14 0 0

= 0,06 -0,08 -0,08 = 0,001344;

0,07 -0,08 -0,20

0,28 0,14 0

= 0 0,06 -0,08 = - 0,001792;

0 0,07 -0,20

0,28 0 0,14

= 0 -0,08 0,06 = - 0,000224.

0 -0,08 0,07

Координаты нового центра будут иметь следующие значения:

x_1C = /∆ = 0,50; x_2C = = -0,67; ∆= -0,08.

Подставив значения x_iC в уравнение (1), определим значение параметра оптимизации в новом центре поверхности отклика Y_C:

Y_C = 0,67 + 0,14^.0,50 – 0,06^.(-0,67) – 0,07^.(-0,08) – 0,14^.(0,50)² –

- 0,04^.(-0,67)² – 0,09^.(-0,08)² – 0,08^.(0,67)^.(-0,08) = 0,73

Таким образом, уравнение (1) после параллельного переноса начала координат в новый центр примет вид:

y = 0,73 – 0,14 – 0,04 – 0,10 – 0,08x₂x₅

Для избавления данного уравнения от последнего члена решим характеристическое уравнение:

(-0,14 – В) 0 0

0 (-0,14 – В) -0,04 =

0 -0,04 (-0,10 – В)

= - В³ – 0,28В² – 0,0208В +0,000168 = 0, или

= В³ + 0,28В² + 0,0208В - 0,000168 = 0

Или с учетом точности эксперимента данное уравнение можно упростить

В² + 0,28В + 0,02 = 0

Тогда В_1,2 = -0,14

В итоге каноническая форма уравнения (1) примет вид:

0,73 – Y = 0,14 + 0,14 , (2)

где Y – значение параметра оптимизации в новой системе координат; x₁ и x₂ – значение факторов в этой же системе.

При этом для перехода к новой системе координат необходимо совершить поворот осей вокруг нового центра на 90⁰.

Таким образом, сложный многофакторный процесс нитроцементации в ЭП в «почти стационарной» области может удовлетворительно описываться квадратичным уравнением с двумя переменными. Полученные данные позволяют выбирать режимы обработки низкоуглеродистой стали для достижения необходимого уровня ее прочности и износостойкости [5,7].

Геометрический образ уравнения (2) изображается в виде изолиний, представляющих собой концентрические окружности с центром в точке С с координатами x_1c = 0,50, x_2c = -0,67, что соответствует ₁ = 0,38 л/мин, ₂ = 1,85 л/мин (рис.1).

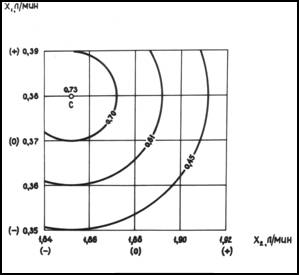
Рис.1. «Почти стационарная» область процесса

нитроцементации в ЭП, характеризуемая уравнением (2)

Литература

1. Wrzaszcz E. Mathematic design of an experiment at the optimization of nitrocementation in the electrostatic field. /Materiały II Międzynarodowej Konferencji Naukowej - Agrolaser 2003. Lublin 2003. - S.93-96.

2. Vzashch E.E., Pivnik L.V. The mathematical design of experiments at optimization of technological processes. //Problemy inżynerii rolniczej w aspekcie rolnictwa zrównoważonego – Materiały Jubileuszowej Międzynarodowej Konferencji Naukowej – Lublin 2005. - S.141-145.

3. Вржащ Е.Э. Математическое планирование эксперимента при решении компромиссных инженерных задач на примере получения качественного диффузионного слоя при нитроцементации стальных изделий в электростатическом поле/ Актуальные вопросы технического, технологического и кадрового обеспечения АПК: Материалы VI научн.-практ. Конф.с междун. участием «Чтение И.П. Терских». Иркутск: Изд-во ИрГСХА, 2014, с.21-26/

4. Вржащ Е.Э. Математическая оптимизация эксперимента при нитроцементации стали в электростатическом поле. Вестник ИрГСХА, 2017. Вып.81/1, август .-с. 91-96.

5. Вржащ Е. Высокотемпературная нитроцементация в электростатическом поле. LAP Lambert, Düsseldorf 2017.

6. Никитина Е.Н. Геометрия поверхностей отклика, представленных полиномами./Сб. «Применение математических методов для исследования многокомпонентных систем». «Металлургия», М., 1974.

7. Vrzhashch E., Suchaeva A. Nitrocarburizing of metallic details in an electrostatic field//Materials of the XII International scientific and practical conference Areas of scientific thought- 2016/2017. Volume 8. Technical science. Construction and architecture. Geography and geology. Sheffield, 2017. Science and education LTD – p.52-58.