Г.Б.Камалова, С.Бейсебаева

Казахский национальный педагогический университет им.Абая, г.Алматы

К ВОПРОСУ ИСПОЛЬЗОВАНИЯ ТЕХНОЛОГИЙ ПАРАЛЛЕЛЬНОГО ПРОГРАММИРОВАНИЯ ПРИ ОБУЧЕНИИ БУДУЩИХ УЧИТЕЛЕЙ ИНФОРМАТИКИ ЧИСЛЕННЫМ МЕТОДАМ

Наличие огромного множества прикладных задач с большим объемом вычислений, необходимость их решения и принципиальная ограниченность максимально возможного быстродействия компьютеров традиционной, ‘фон Неймановской’, архитектуры привели к разработке и использованию суперкомпьютеров, которые благодаря многопроцессорности позволяют одновременно, в один и тот же момент времени осуществить выполнение нескольких операций обработки данных. Разделение при этом применяемого вычислительного алгоритма на информационно независимые части и организация выполнения каждой выделенной части вычислений на разных процессорах, позволяет выполнить необходимые вычисления с меньшими затратами времени и в целом достичь ускорения процесса решения задачи.

Широкое распространение подобные параллельные вычисления приобрели с переходом компьютерной индустрии на массовый выпуск многоядерных процессоров с векторными расширениями. Сегодня ими оснащены практически все устройства, начиная от карманных гаджетов и до самых мощных суперкомпьютеров. Развитие вычислительной техники с необходимостью подкрепляется совершенствованием алгоритмической и программной компонент – технологий параллельного программирования. Одним из серьезных препятствий к их применению является недостаточность специалистов, умеющих использовать возможности многопроцессорных устройств, изначальная нацеленность их мышления на строгую последовательность выполнения вычислений. Поэтому в сложившейся ситуации остро встает проблема подготовки кадров в области параллельного программирования и параллельных вычислений. Причем подготовка в данной области должна начинаться как можно раньше, со школы, а это требует соответствующей подготовки учителя информатики.

Содержание и методика обучения теории параллельных вычислений является новым для педагогических вузов, и, как показывает анализ исследований по данному направлению, а также содержания программ подготовки будущих учителей информатики в области параллельных вычислений и многопроцессорных ЭВМ, вопросы, касающиеся данной теории, не отражены в них в достаточной мере. Исходя из этого, целью данного исследования является обоснование возможности и целесообразности использования технологий параллельного программирования при обучении будущих учителей информатики численным методам.

Являясь элементом вычислительной информатики [1], параллельные вычисления и параллельное программирование затрагивают многие вопросы решения вычислительных задач на компьютере. Изучение их не просто актуально сегодня, но и может служить одним из возможных путей усиления фундаментальной подготовки специалистов в области информатики, в том числе и будущих учителей информатики. И могут быть предметом изучения ряда дисциплин предметной их подготовки.

Часть вопросов, связанных с разработкой, анализом и реализацией параллельных алгоритмов может с успехом рассматриваться в курсе «численные методы». Это – одна из самых выигрышных дисциплин в системе подготовки будущих учителей информатики в деле получения не только навыков решения вычислительных задач, но и опыта практической работы на современных электронных вычислительных машинах и изучения областей их применения. В ней можно объединить рассмотрение как последовательных, так и параллельных алгоритмов. Разумеется, что разработка параллельных алгоритмов и программ является непростой задачей в связи с трудностью выявления параллелизма, обычно скрытого, в алгоритме, т.е. выявления частей алгоритма, могущих выполняться независимо друг от друга. Но, разработанное за десятилетия эксплуатации вычислительной техники огромное количество тщательно отлаженных и оптимизированных последовательных алгоритмов, может быть положено в основу параллельных алгоритмов и использовано для сравнения эффективности распараллеливания. Потенциальная возможность распараллеливания неодинакова для вычислительных задач различного типа – она значительна для задач, содержащих большой объем независимых друг от друга вычислений, а задачи, рассматриваемые в курсе «численные методы» практически все такие. Программу его составляют достаточно традиционные учебные разделы, содержащие тщательно отлаженные и оптимизированные последовательные алгоритмы решения типовых задач вычислительной математики. Это, во-первых, численные методы решения основных задач линейной алгебры, к которым, как правило, в итоге сводится решение большинства задач вычислительной математики. Кроме того, основные численные методы решения задач математического анализа, задач для дифференциальных уравнений, обыкновенных и в частных производных, а также обработки экспериментальных данных. Обучение им немыслимо без активного использования компьютера и его программного обеспечения.

Распараллеливание алгоритмов и их компьютерная реализация требует намного более серьезного и углубленного анализа структуры алгоритмов, нежели при традиционно-последовательном программировании. В стандартную схему решения задачи на ЭВМ с учетом специфики параллельных вычислений необходимо включить еще несколько пунктов: информационный анализ; распараллеливание процессов; конструирование параллельной программы и оценка эффективности параллельной программы» [2].

Информационный анализ позволяет выяснить те части программы, выполнение которых возможно организовать параллельно, независимо друг от друга, а процесс распараллеливания может быть организован следующим образом: сначала между процессорами распределяются операции, которые зависят только от внешних данных программы, не зависят друг от друга и могут быть выполнены одновременно. Это образует первый ярус ярусно-параллельной формы графа алгоритма, обычно использующейся при распараллеливании алгоритмов. Второй ярус включает операции, зависящие только от операций первого яруса и т.д.

В качестве примера приведем одну из задач курса «численные методы» – задачу численного интегрирования, где требуется вычислить определенный интеграл методом центральных прямоугольников:

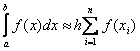, , , использование которого приводит к необходимости сложения значений функций .

Заметим, что в данном алгоритме вычисления интеграла заключен немалый параллелизм. Во-первых, вычисление значений x_i не зависит друг от друга, независимо друг от друга вычисляются и соответствующие им значения функции , поэтому выполнение их возможно организовать параллельно на разных процессорах. Далее, поскольку неважно, в каком порядке суммируются элементы, можно частичное суммирование производить параллельно на разных процессорах, а потом складывать результаты частичных сумм, в соответствии с обычно использующейся при распараллеливании алгоритмов ярусно-параллельной формой графа алгоритма.

Построение параллельной программы предполагает выбор подходящей технологии программирования и реализации на ее основе разработанного параллельного обобщения традиционного последовательного алгоритма. Наиболее распространенными технологиями параллельного программирования, базирующимся на традиционных языках программирования С/С++, в настоящее время являются OpenMP – для компьютеров с общей памятью и MPI (Message Passing Interface - интерфейс передачи сообщений) – для кластерных систем и компьютеров с распределенной памятью, который может применяться также и на вычислительных системах других типов. Их использование требует владения студентами базовыми знаниями и навыками разработки программ на данных языках программирования, которые изучаются, как правило, на первых курсах обучения в педагогических вузах.

Одним из наиболее эффективных подходов к обучению будущих учителей информатики разработке параллельных алгоритмов и использованию технологий параллельного программирования в рамках курса численные методы может быть применение метода проектов. Организация самостоятельной учебной деятельности студентов в свете современных тенденций развития высшего образования имеет особое значение, так как современное общество ставит перед высшей школой задачу подготовки не только знающего, но и, главным образом, мыслящего и умеющего добывать самостоятельно необходимые для практической деятельности знания и умения специалиста. В качестве индивидуальных или групповых проектов в рамках данного курса студентам могут быть предложены темы, связанные с разработкой и реализацией параллельного обобщения традиционных последовательных алгоритмов, рассматриваемых на аудиторных занятиях.

Таким образом, технологии параллельного программирования могут с успехом использоваться в обучении параллельным алгоритмам решения типовых задач вычислительной математики в курсе численные методы, что позволит расширить круг знаний будущих учителей информатики о современных компьютерных системах, технологиях программирования и возможностях их использования для эффективного решения вычислительных задач.

1 Ильин В.П. Вычислительная информатика: открытие науки.– Новосибирск: Наука, Сиб. отделение, 1991. – 198с.

2 Анисимова Н.С., Слива М.В. Этапы решения задачи на ЭВМ при параллельном программировании // Информатика и образование, 2007. – №2. – С.68-70