Д. т. н. Бакиров Ж.Б., к. т. н. Танирбергенова А.А.

Карагандинский государственный технический университет, Казахстан

Казахстанский агротехнический университет, Казахстан

ПРОЕКТНЫЙ РАСЧЕТ КОНСТРУКЦИЙ

ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

Последним этапом расчета на прочность при случайных воздействиях является определение надежности и сравнение с нормативной. Если надежность конструкции равна нормативной или приемлемо больше нее, то расчет заканчивают. Если этого нет, то необходимо менять размеры и делать перерасчет до тех пор, пока надежность конструкции не станет приемлемой. Вместо этого целесообразно разработать методику расчета, по которой требуемая надежность заранее закладывается в проектируемую конструкцию. Для этого геометрические параметры конструкций должны быть определены из условия равенства ее надежности заданному значению Н_*.

Вопросы расчета надежности технических систем рассмотрены в работах А.Р. Ржаницина, В.В. Болотина и других и подробно изложены в монографии [1]. Некоторые аспекты проектирования элементов конструкций при действии случайных воздействиях рассмотрены в работе [2]. В развитие этих исследований в данной работе в общем виде получены соотношения для определения обобщенной геометрической характеристики сечения элемента конструкций по заданной надежности при случайных изменениях расчетных и предельных напряжений.

Для упругих систем максимальные (расчетные) напряжения в опасном сечении S в общем виде можно записать так:

, (1)

где q – обобщенный параметр, имеющий смысл нагрузки;

К – параметр, зависящий от геометрических параметров конструкции.

Конкретный вид этих параметров получаем в ходе решения детерминированной задачи о напряженно-деформированном состоянии конструкции. Так, в курсе сопротивления материалов q представляет собой внутренний силовой фактор, а параметр к – одну из геометрических характеристик поперечного сечения: при растяжении-сжатии и срезе он равен площади, при кручении и изгибе – соответствующим моментам сопротивления. Внутренний силовой фактор может быть выражен через внешние нагрузки методом сечения.

Пусть на конструкцию действует случайная нагрузка с известным законом распределения Р(q). Тогда закон распределения максимальных напряжений можно найти по формуле преобразования вероятностей

. (2)

При таком преобразовании законы распределения напряжения и нагрузки совпадают, а изменяются лишь параметры распределения. Для нормального закона они преобразуются следующим образом:

m_s=m_q/К, _s=_q/К. (3)

Надежность конструкций будем трактовать как вероятность ее безотказной работы. Если предельное напряжение R детерминированная величина, то надежность определятся соотношением

, (4)

где F(S) – функция распределения расчетных (максимальных) напряжений.

Если действующие и предельные напряжения являются случайными величинами с известными законами распределения и , то для определения надежности можно использовать выражения, приведенные в работах [1, 2]:

. (5)

Используя эти соотношения, получаем уравнение, связывающее надежность с геометрической характеристикой сечения K

(6)

где a_i – заранее известные параметры законов распределения нагрузки и предельного напряжения.

Приравнивая далее надежность заданному значению, определяем параметр К

(7)

Иногда уравнение (7) невозможно решить относительно К. Для определения величины К в этом случае удобнее использовать графический метод. Задаваясь значениями К_i, из выражения (7) находим соответствующие надежности Н_i. По этим данным строим график зависимости (7). Из этого графика находим значение К, соответствующее заданной надежности. При известном значении К легко найти размеры поперечного сечения при любом виде деформаций.

Пусть предельное напряжение R является детерминированной величиной. Тогда уравнение, связывающее заданную надежность с геометрическими параметрами сечения примет вид

Н_*= F (R).

где F(S) – функция распределения расчетных (максимальных) напряжений.

Рассмотрим различные законы распределения нагрузки.

1. Нормальный закон. Используя выражение для функции распределения и формулы (3), получаем

Отсюда имеем

где g_н– квантиль нормального распределения (гауссовский уровень надежности), соответствующий вероятности Н_*.

2. Логарифмически нормальный закон. Используя соотношения, связывающие параметры распределения нагрузки и напряжения, а также связь между параметрами распределения и числовыми характеристиками нагрузки (σ_q, m_q, k_q= σ_q/m_q), получаем [1]

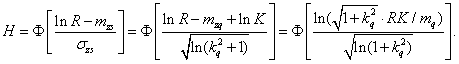
Отсюда имеем .

3. Гамма-распределение. Функцией распределения этого закона является функция "хи-квадрат", табулированная Пирсоном [3]. С учетом этого

Отсюда имеем

где квантиль «хи-квадрат» распределения со степенью свободы соответствующей надежности H_*; a_q, b_q - параметры распределения нагрузки.

4. Закон Вейбулла. Используя выражение для функции распределения и связь между параметрами распределения нагрузки и напряжения, получаем

Отсюда имеем .

Пусть наряду с нагрузкой и предельные напряжения являются случайной величиной. Рассмотрим различные сочетания законов их распределения.

1. Если нагрузка и предельное напряжение распределены по нормальному закону, то надежность определяется функцией распределения нормального закона с аргументом

.

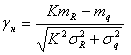Решая это уравнение относительно К, получаем

2. Если нагрузка и несущая способность распределены по логарифмически нормальному закону, то аналогично имеем

.

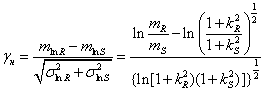Отсюда с учетом того, что , получаем

3. Нагрузка и несущая способность распределены по закону Вейбулла. Надежность конструкции определяется выражением

где .

Для определения К при известных параметрах распределения нагрузки и прочности численным методом определяется значение интеграла и строится график зависимости надежности от параметра К. Из этого графика по заданной надежности определяется значение геометрической характеристики, обеспечивающего заданную надежность конструкций.

Литература

1. Бакиров Ж.Б. Вероятностные методы расчета элементов конструкций. Караганда: КарГТУ, 2001. - 180 с.

2. Капур К., Ламберсон Л. Надежность и поектирование систем. – М.: Мир, 1980. – 604 с.

3. Справочник по специальным функциям / Под ред. М. Абрамовица и И Стиган. М.: Наука, 1979. -830 с.