Пиль Э.А.
Академик РАЕ, д.т.н., профессор
РАЗЛИЧНЫЕ ПУТИ ВЫХОДА ИЗ ЭКОНОМИЧЕСКОГО
КРИЗИСА
Ранее в своих статьях
автор показал, что для описания процессов, происходящих в экономике страны, ее можно
представить в виде объема экономической оболочки. В данной статье автор
рассматривает ВВП (GDP) страны как площадь поверхности экономической оболочки Ssl.
Расчет валового
внутреннего продукта ВВП (GDP) может быть рассчитан путем вычисления площади
поверхности Ssl, на которую действуют внешние силы Р. При расчетах использовались три
переменные, т.е. Ssl (GDPsl) = f(Х1, Х2, Х3).
Здесь Х1, Х2 и Х3 переменные влияющие на расчет ВВП (GDP) страны.
Следует сразу
отметить, что при расчетах и построении рисунков переменные Х1, Х2 и Х3 могли
бить величинами постоянными, уменьшаться или увеличиваться в 10 раз. На основе произведенных
расчетов было построено 27 графиков, которые можно подразделить на следующие
четыре группы:
· значения переменных Х1,
Х2 и Х3 постоянные и увеличиваются;
· значения переменных Х1,
Х2 и Х3 постоянные и уменьшаются;
· значения переменных Х1,
Х2 и Х3 уменьшаются и увеличиваются;
· значения переменных Х1,
Х2 и Х3 постоянные, увеличивающиеся и уменьшающиеся.
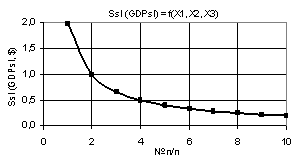
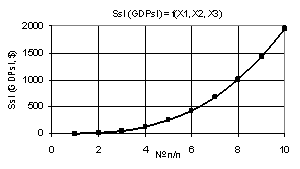
На рис. 1
представлен двухмерный график зависимости Ssl (GDPsl) при Х1
= Х2 = 1 и Х3 = 1…10, из которого видно, что значения
Ssl вначале интенсивно падают со значения 1.96 до 0.39 в точке 5,
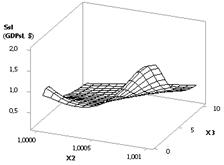
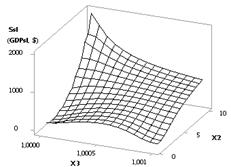
а потом идет их плавное уменьшение до 0.2. На рис. 2 показан
3D-график, который позволяет
более наглядно представить изменения Ssl. В этом случае нам целесообразно
иметь значение до второй точки, т.к. в точке 2 величина Ssl (GDPsl) уже равна 0.98, т.е. меньше
единицы, что означает падение ВВП (GDP). Рисунок 2 построен при использовании
переменных Х2 и Х3, т.е. Ssl (GDPsl) = f(Х2, Х3).
|
Рис. 1. Зависимость Ssl (GDPsl) = f(Х1,
Х2, Х3) при Х1 = Х2 = 1, Х3 = 1…10 |
Рис. 2. 3D-график: Ssl
(GDPsl) = f(Х2, Х3) |
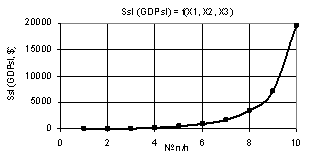
Из
следующего рис. 3 видно, что при Х1 = Х2 = 1…10 и
Х3 = 1 построенная кривая Ssl увеличивается по
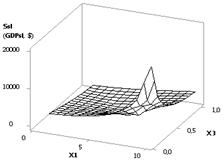
параболе с 1.96 до 1960.23, т.е. в 1000 раз. На рис. 4 показана зависимость в
виде трехмерного графика. Здесь следует сразу отметить, что вид 3D-графика зависит
от выбора последовательности используемых осей. Исходя из рисунка 3 видно, что нам
целесообразно иметь значения крайних правых точек,
т.к. при них величина Ssl (GDPsl) будет максимальной.
Из
построенной кривой на рис. 5 видно, что здесь значения Ssl (GDPsl) при
Х1 = Х2 = 1…10, Х3 = 1…0.1 принимают достаточно большую величину, начиная с 1.96
и заканчиваясь 19602.23, т.е. они увеличились в 10000 раз. На рис. 6 показан
построенный 3D-график.
|
Рис. 3. Зависимость Ssl (GDPsl) = f(Х1,
Х2, Х3) при Х1 = Х2 = 1, Х3 = 1…10 |
Рис. 4. 3D-графики: Ssl (GDPsl) = f(Х3, Х2); при Х1 =
Х2 = 1…10, Х3 = 1 |
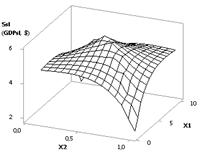
Из следующего рис. 9
видно, что здесь значения Ssl вначале
растут с 1.96 до своего максимума 3.84 в точке 4, после чего они постепенно
падают до величины 0.2, т.е. уменьшаются в 19.6 раза. На рис. 10 показаны три 3D-графика для Ssl (GDPsl)
= f(Х1, Х2), Ssl (GDPsl) = f(Х3, Х1) и Ssl (GDPsl)
= f(Х3, Х2) соответственно.
|
Рис. 5.
Зависимость Ssl
(GDPsl)
= f(Х1, Х2, Х3) при Х1 = Х2 = 1…10, Х3 = 1…0.1 |
Рис. 6. 3D-график: Ssl (GDPsl) = f(Х1, Х3); при Х1 = Х2 = 1…10, Х3 = 1…0.1 |
|
Рис. 7. Зависимость Ssl (GDPsl) = f(Х1, Х2,Х3) при Х1 = 1…10, Х2 = Х3 = 1…0.1 |
Рис. 8. 3D-графики: Ssl (GDPsl) = f(Х2, Х1) при Х1 = 1…10, Х2 = Х3 = 1…0.1 |
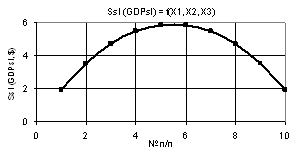
На рис. 7 показана
зависимость Ssl (GDPsl) при Х1 = 1…10, Х2 = Х3 = 1…0.1. Как
видно из рисунка вначале значения Ssl (GDPsl) увеличиваются с 1.96 до
максимального значения 5.88, т.е. в 3 раза, после чего уменьшаются опять до
1.96. При данных значениях переменных целесообразно выбирать крайние значения около
максимума, т.е. между точками 4 и 7.
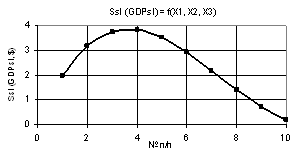
Рис. 9. Зависимость Ssl (GDPsl) = f(Х1, Х2, Х3)
при Х1 = 1…10, Х2 = 1…0.1, Х3 = 1
|
а |
б |
с |
|
Рисунок 10. 3D-графики: a - Ssl (GDPsl) = f(Х1, Х2); b - Ssl
(GDPsl) = f(Х3,
Х1) с - Ssl (GDPsl) = f(Х3, Х2) при Х1 = 1…10, Х2 = 1…0,1, Х3 = 1 |
||
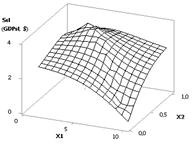
Из рисунка 11 видно, что
построенная кривая Ssl (GDPsl) постепенно растет со значения 1.96
до своего максимума Sslmax = 38.42 в точке 7, после чего уменьшается почти в 2
раза до величины 19.36. Этот рисунок был построен при следующих значениях
переменных Х1 = 1…0,1, Х2 = 1…10, Х3 = 1.
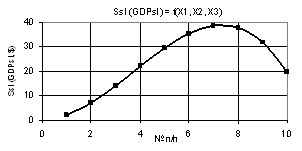
Рис. 11. Зависимость Ssl (GDPsl) = f(Х1, Х2, Х3)
при Х1 = 1…0,1, Х2 = 1…10, Х3 = 1
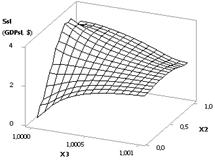
На последнем рисунке 12
представлены три трехмерных графика Ssl (GDPsl).
После того как были
произведены расчеты их результаты были сведены в сводную таблицу 1, в которой
получилось 31 строка, не смотря на то, что было построено 27 двумерных графика.
Это связано с тем, что ряд построенных графиков имели максимумы. В данную
сводную таблицу были введены такие отношения как:
·
Sslb… Sslf, где Sslb - начальное значение площади
поверхности экономической оболочки, ед.2;
Sslf -
конечное значение площади поверхности экономической оболочки, ед.2;
·
Sslf /Sslb -
отношение конечного значения площади поверхности экономической оболочки к
начальному.
|
|
|
|
|
Рис. 12. 3D-графики: a - Ssl (GDPsl) = f(Х2, Х1); b - Ssl
(GDPsl) = f(Х1,
Х3); c - Ssl (GDPsl) = f(Х2, Х3) при Х1 = 1…0.1, Х2 = 1…10, Х3 = 1 |
||
Отношение конечного значения площади поверхности экономической
оболочки Sslf к начальному Sslb показывает, во
сколько раз увеличились (уменьшились) их значения под воздействием различных
внешних сил. Следовательно, имея эти данные, мы можем выбрать такие значения
переменных Х1, Х2 и Х3, при которых площадь поверхности экономической оболочки
останется неизменным или даже увеличится под воздействием внешних сил. То есть, тем самым при экономическом кризисе выбранные значения
переменных позволят сохранить на прежнем уровне, или даже увеличить ВВП (GDPsl) страны. После того, как
была построена сводной таблица с 31 строками, ее преобразовали следующим образом, оставили
только те значения, где Sslf /Sslb
≥ 1. На основе этого преобразования была получена
окончательная сводная таблица, в которую вошли
17 строк. Таким образом, было получено 17 вариантов, позволяющих странам
выйти из очередного экономического кризиса, которые сведены в таблицу 2, где отношения Sslf /Sslb в последнем столбце расположены по убыванию.
Как видно из табл. 1 есть три варианта, при которых ВВП (GDPsl) страны не изменится в период экономического кризиса это строки 15, 16 и 17, где отношения Sslf /Sslb = 1.
В остальных 14 вариантах можно получить даже увеличение ВВП (GDPsl) в 10000 раз.
Теперь
преобразуем таблицу 1 в таблицу 2 для чего сгруппируем строки по количеству
переменных, входящих в них. Таким образом, в таблице 2 получились следующие
четыре группы: с 1 переменной; с 2 переменными и все переменные.
|
Таблица 1. Статистика отношений Sslf /Sslb where Sslf /Sslb ≥ 1 |
|||||
|
№ п/п |
X1sl, ед. |
X2sl, ед. |
X3sl, ед. |
Sslb … Sslf, ед.2 (GDPslb…GDPslf , $) |
Sslf /Sslb
(GDPslf /GDPslb) |
|
1. |
1…10 |
1…10 |
1…0.1 |
1.96…19602.33 |
10000.0 |
|
2. |
1…10 |
1…10 |
1 |
1.96…1960.23 |
1000.0 |
|
3. |
1 |
1…10 |
1…0.1 |
1.96…1960.23 |
1000.0 |
|
4. |
1…10 |
1…10 |
1…10 |
1.96…196.02 |
100.0 |
|
5. |
1 |
1…10 |
1 |
1.96…196.02 |
100.0 |
|
6. |
1…0.1 |
1…10 |
1…0.1 |
1.96…196.02 |
100.0 |
|
7. |
1…10 |
1 |
1…0.1 |
1.96…196.02 |
100.0 |
|
8. |
1…0.1 |
1…10 |
1 |
1.96…38.42 |
19.60 |
|
9. |
1 |
1…10 |
1…10 |
1.96…19.60 |
10.0 |
|
10. |
1…10 |
1 |
1 |
1.96…19.60 |
10.0 |
|
11. |
1 |
1 |
1…0.1 |
1.96…19.60 |
10.0 |
|
12. |
1…10 |
1…0.1 |
1…0.1 |
1.96…5.88 |
3.0 |
|
13. |
1…0.1 |
1…10 |
1…10 |
1.96…5.88 |
3.0 |
|
14. |
1…10 |
1…0.1 |
1 |
1.96…3.84 |
1.96 |
|
15. |
1 |
1 |
1 |
0.26…0.26 |
1.0 |
|
16. |
1…10 |
1 |
1…10 |
1.96…1.96 |
1.0 |
|
17. |
1…0.1 |
1 |
1…0.1 |
1.96…1.96 |
1.0 |
Таким образом, таблица 2, в зависимости
от применения количества переменных, позволяет нам использовать различное
количество вариантов:
·
с 1 переменной (3 варианта);
·
с 2 переменными (8 вариантов);
·
все переменные (5 вариантов).
Как видно самое большое количество
вариантов приходится на две переменные. Но если использовать все переменные для
выхода из экономического кризиса, то в этом случае мы получим самый большой
экономический эффект.
Ввиду того, что переменная
Х2 характеризует толщину экономической оболочки, поэтому если принять ее за
единицу (Х2 = 1), то тогда табл. 2 превратиться в табл. 3, в которой вместо 16
будет уже только 5 строк. Переменную Х2 можно охарактеризовать как отношение
курса национальной валюты к валюте, используемой при международных расчетах
(доллар, евро и др.)
|
Таблица
2. Статистика переменных для Sslf /Sslb по убыванию по
группам |
|||||
|
№ п/п |
X1sl, ед. |
X2sl, ед. |
X3sl, ед. |
Sslb … Sslf, ед.2 (GDPslb…GDPslf , $) |
Sslf /Sslb
(GDPslf /GDPslb) |
|
1 переменная |
|||||
|
1.
|
1 |
1…10 |
1 |
1.96…196.02 |
100.0 |
|
2.
|
1…10 |
1 |
1 |
1.96…19.60 |
10.0 |
|
3.
|
1 |
1 |
1…0.1 |
1.96…19.60 |
10.0 |
|
2 переменные |
|||||
|
4.
|
1…10 |
1…10 |
1 |
1.96…1960.23 |
1000.0 |
|
5.
|
1 |
1…10 |
1…0.1 |
1.96…1960.23 |
1000.0 |
|
6.
|
1…10 |
1 |
1…0.1 |
1.96…196.02 |
100.0 |
|
7.
|
1…0.1 |
1…10 |
1 |
1.96…38.42 |
19.60 |
|
8.
|
1 |
1…10 |
1…10 |
1.96…19.60 |
10.0 |
|
9.
|
1…10 |
1…0.1 |
1 |
1.96…3.84 |
1.96 |
|
10.
|
1…10 |
1 |
1…10 |
1.96…1.96 |
1.0 |
|
11.
|
1…0.1 |
1 |
1…0.1 |
1.96…1.96 |
1.0 |
|
Все переменные |
|||||
|
12.
|
1…10 |
1…10 |
1…0.1 |
1.96…19602.33 |
10000.0 |
|
13.
|
1…10 |
1…10 |
1…10 |
1.96…196.02 |
100.0 |
|
14.
|
1…0.1 |
1…10 |
1…0.1 |
1.96…196.02 |
100.0 |
|
15.
|
1…10 |
1…0.1 |
1…0.1 |
1.96…5.88 |
3.0 |
|
16.
|
1…0.1 |
1…10 |
1…10 |
1.96…5.88
|
3.0 |
|
Таблица
3. Статистика переменных для Sslf /Sslb, где Sslf /Sslb ≥ 1 и X2sl = 1 по убыванию по группам |
|||||
|
№ п/п |
X1sl, ед. |
X2sl, ед. |
X3sl, ед. |
Sslb … Sslf, ед.2 (GDPslb…GDPslf , $) |
Sslf /Sslb (GDPslf /GDPslb) |
|
1 переменная |
|||||
|
1.
|
1…10 |
1 |
1 |
1.96…19.60 |
10.0 |
|
2.
|
1 |
1 |
1…0.1 |
1.96…19.60 |
10.0 |
|
2 переменные |
|||||
|
3.
|
1…10 |
1 |
1…0.1 |
1.96…196.02 |
100.0 |
|
4.
|
1…10 |
1 |
1…10 |
1.96…1.96 |
1.0 |
|
5.
|
1…0.1 |
1 |
1…0.1 |
1.96…1.96 |
1.0 |

 а
а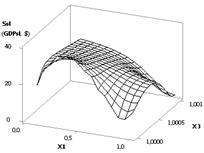 б
б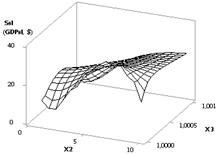 с
с