Экономические науки/2. Банки и банковская система

Коляков М. А., Челышев Д. С.

Российский экономический университет им. Г.В. Плеханова, Россия

Анализ кривой VaR для анализа российского банка

Методология Value-at-Risk (VaR) получила широкое распространение не только в зарубежной, но и российской банковской практике. Являясь стоимостной мерой риска, VaR показывает такую величину, которую не превысят потери с заданной вероятностью. 3 базовых параметра VaR представляют собой временной горизонт, доверительный уровень и базовую валюту. Временной горизонт расчета показателя VaR зависит от выбранной методики (базельская методология отличается от Risk Metrics). Уровень допустимого риска, или доверительный уровень, указывает на квантиль распределения, который будет использован в расчете (в более консервативных практиках - 95%). Показатель базовой валюты должен быть определен экспертом самостоятельно; в случае с анализом рисков иностранных контрагентов, полезно воспользоваться случайными процессами (stochastic processes) и смоделировать вероятный обменный курс на дату валютирования.

В данной статье авторами предлагается рассмотреть типовой анализ распределений котировок российских банков (на примере банка «Санкт-Петербург»); затем, выявив наилучшее распределение, провести оценку VaR и Expected Shortfall (ES) и проверить качество полученных оценок.

Авторами были выбраны следующие распределения для описания выборки значений доходности банка (ежедневные доходности рассматриваются за период с января 2012 года по ноябрь 2016 года – всего 1225 значений): нормальное распределение, t-распределение, гиперболическое распределение, обобщенное гиперболическое распределение.

Результаты оценки распределений представлены на рисунке ниже.

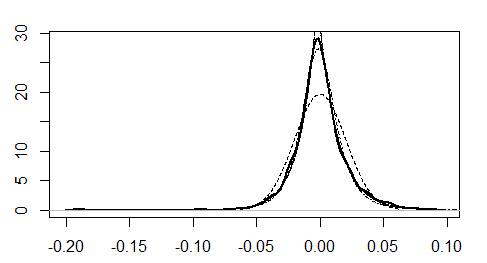
Рис. 1. Оценка распределений временного ряда банка «Санкт-Петербург».

Для отыскания распределения, наиболее подходящего для описания доходностей временных рядов, был использован информационный критерий Акаике.

В общем случае критерий формулируется следующих образом:

,

где k – количество параметров модели, L - максимизированное значение функции правдоподобия модели.

По результатам оценки наилучшим признано гиперболическое распределение. Значения информационного критерия Акаике для гиперболического, обобщенного гиперболического распределения и t-распределения Стьюдента близки, но значительно меньше, чем у нормального распределения.

Определив наилучшее распределение для каждого временного ряда, перейдем к оценке VaR и ES (Expected Shortfall).

Value-at-Risk (грань потерь)	Expected Shortfall (ожидаемые потери)

Таблица 1. Формулы используемых мер риска.

Воспользуемся методом Монте-Карло (объем моделируемой выборки – 1000000 значений, уровень значимости задан на уровне 0.05) для оценки VaR и ES, основываясь на полученных ранее распределениях:

	Стоимостная оценка риска
VaR	- 0.034
ES	- 0.048

Таблица 2. Итоговые значения VaR и ES.

Далее построим кривую VaR, которая используется для тестирования качества оценок. Она состоит из набора последовательных во времени значений VaR. Для этого разделим выборку обучающую (T1) и экзаменующую (T2). Объем обучающей выборки будет составлять 780 значений. Рассмотрим два варианта построение кривой VaR.

В первом случае для каждых 780 значений будет оцениваться параметры нормального распределения с дальнейшим моделирование распределения с помощью метода Монте-Карло (объем моделируемой выборки – 1000000 значений, уровень значимости задан на уровне 0.05).

Во втором случае для каждых 780 значений были оценены параметры 4 описанных выше распределений с выбором лучшего на основе информационного критерия Акаике с дальнейшим моделированием распределения с помощью метода Монте-Карло (объем моделируемой выборки – 1000000 значений, уровень значимости задан на уровне 0.05).

Для оценки полученных кривых в обоих случаях воспользуемся тестом Купика. Тест состоит в сравнении модельной и эмпирической частот превышений фактическими убытками границы VaR:

Гипотеза:

Статистика:

Построим кривые VaR для временных рядов:

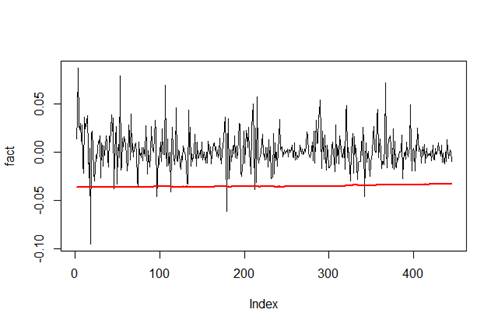
Рис. 2. Кривая VaR с подбором распределения на основе критерия Акаике временного ряда банка «Санкт-Петербург».

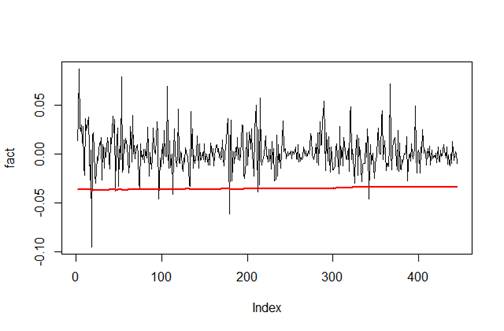
Рис. 3. Кривая VaR, построенная на основе нормального распределения временного ряда банка «Санкт-Петербург».

Подбор лучшего распределения на основе критерия Акаике	0.04%
Нормальное распределение	0.01%

Таблица 3. Тест Купика для кривых VaR

По полученным результатам видно, что гипотеза о совпадении модельной и эмпирической частот превышений фактическими убытками границы VaR при моделировании с помощью нормального распределения значительно ниже, чем при использование гиперболического распределения.

Можно заключить, что использование гиперболического и обобщенного гиперболического распределения при моделировании распределения доходностей акций коммерческих банков себя оправдывает. Данный подход позволят как оценить границу потерь, так и ожидаемые потери. Интересен и тот факт, что данные распределения лучше описывают «хвосты» распределений, позволяя получать более точную оценку.