Повышение качества генераторов псевдослучайных последовательностей на основе формализованных моделей дискретных отображений класса «клеточные автоматы»
Кандидат технических наук, старший научный сотрудник отдела СПМО МОУ «ИИФ» Коваленко М.П., кандидат технических наук, начальник отдела СПМО МОУ «ИИФ» Рязанцев А.М., инженер-программист отдела СПМО МОУ «ИИФ» Коваленко А.П.
Введение
Опыт решения различных задач, связанных с созданием систем криптографической защиты информации, ее обработки и передачи, а также многоуровневых систем санкционированного управления распределенными объектами, систем идентификации удаленных объектов, показывает очевидные преимущества использования генераторов, работающих в режиме групповой генерации, то есть вырабатывающих случайные векторы или группы независимых случайных чисел.
Одним из таких генераторов является генератор, построенный с использованием формализованных моделей дискретных отображений класса «клеточные автоматы».
Понятие клеточного автомата (КА) появилось в конце сороковых годов 20 века. Оно было сформулировано и определено Джоном фон Нейманом и Конрадом Цусе независимо друг от друга как универсальная вычислительная среда для построения, анализа и сравнения характеристик алгоритмов.
В настоящее время КА являются достаточно развитым направлением дискретной математики. Особый интерес к КА проявляется, прежде всего, благодаря их простоте: на основе простых правил КА могут порождать сложное поведение. Кроме того, КА – это идеальный вариант для параллельных вычислений, они могут эффективно использоваться в многопроцессорных системах или быть реализованы аппаратно, так как основное свойство их правил – локальность и однородность.
КА могут работать в нескольких измерениях: они могут обрабатывать вектор состояний клеток, плоскость или трехмерную модель. Во всех случаях для визуализации работы автомата часто добавляют дополнительное измерение – время, которое позволяет оценить изменения состояний его поля в динамике.
Идея использования КА для криптографического преобразования информации не нова и берет свое начало в 80-х годах 20 века. Одна из первых публикаций по этой теме датируется 1986 годом – известная работа С. Вольфрама [1] дает детальный пример генератора случайных чисел (ГСЧ) на базе одномерного КА, формирующего псевдослучайную последовательность (ПСП) Фибоначчи. Это направление получило развитие в работах [2, 3, 4, 5, 6 и др.], показав практические аспекты применения этой идеи. В конце 90-х годов прошлого столетия стали появляться работы, посвященные построению генераторов ПСП на базе двумерных КА [6, 7, 8 и др.].
В ряде работ [9, 10, 11, 12, 13] были исследованы статистические свойства генераторов ПСП на основе, как одномерных, так и двумерных моделей КА. Полученные при этом результаты свидетельствует о высоких статистических свойствах последовательностей.
Применительно к вопросам защиты информации КА имеют широкий спектр практических приложений. Начиная от задач шифрования и постановки электронной цифровой подписи и до специальных программно-математических преобразований, применяемых для выработки имитовставок, расчета ключевых величин и специальных кодовых дополнений, которые могут быть использованы в системах защиты от несанкционированного задействования (применения) различного рода объектов или в системах их идентификации (опознавания) по информационному или физическому каналу.
Формализованное описание моделей дискретных отображений класса «клеточные автоматы»
Дискретные отображения класса КА относятся к одному из видов дискретных динамических систем, поведение которых полностью определяется в терминах локальных взаимозависимостей их состояний [14, 15].
В общем виде КА представляют собой совокупность клеток, одинаковым образом соединенных между собой в пространстве. Все клетки образуют равномерную сеть (решетку) КА, каждая ячейка, или клетка, которой содержит один или несколько бит данных. Изменение состояния каждой клетки происходит в дискретные моменты времени по определенному закону в зависимости от того, каким было состояние самой клетки и её ближайших соседей по решетке в предыдущий дискретный момент времени.
В общем случае клеточный автомат определяется следующей совокупностью объектов:
A = {G, S, Q, R}, (1)
где G – дискретное метрическое пространство над дискретным множеством элементов, называемое решеткой автомата, а каждый ее элемент называется клеткой и обозначается а, S – множество возможных состояний клетки, Q – окрестность клетки, R – правило перехода.
Как правило, пространство G является одно-, двух- или трёхмерным, но может быть и большей размерности. В зависимости от вида пространства КА делятся на одно-, двух- или трёхмерные КА и т.д.
Решетка представляет из себя однородную структуру, являющуюся конечным множеством клеток аi, перенумерованных последовательно: i = 1, 2, …, N, где N – число элементов (клеток) пространства G.
Для одномерного КА (ОКА): N – число клеток в строке пространства G1.
Для двумерного КА (ДКА): N = n·m, если n = m, то N = n2, где n, m – соответственно число строк и столбцов в G2.
Для трехмерного КА (ТКА): N = n·m·u, если n = m = u, то N = n3, где n, m, u – соответственно число строк, столбцов и слоёв в G3.
В данной статье ограничимся рассмотрением только ДКА.
Применительно к ДКА можно сказать, что n ограничивает пространство G по вертикали, а m – по горизонтали. В результате этих ограничений могут иметь место краевые эффекты – клетки, стоящие на границе решётки, будут отличны от остальных по числу соседей. Для устранения в ДКА краевых эффектов решетка может «заворачиваться» в тор (рисунок 1), т.е. первая строка считается продолжением последней, а последняя – предшествующей первой. То же самое относится и к столбцам решетки.
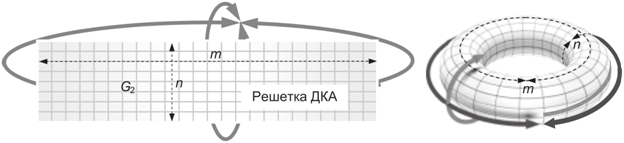
Рисунок 1 – Решетка ДКА, свернутая в тор
Состояние отдельно взятой i-ой клетки в момент времени t характеризуется некоторой переменной si(t) ∈ {S}, где S – конечное множество возможных состояний клеток. Совокупность состояний всех N клеток решетки КА в момент t, определяет состояние решётки (состояние пространства G в момент t), которое обозначается как Аt. Любое состояние Аt является элементом множества L = SN, определяющего множество возможных состояний решетки КА. Применительно к ДКА состояние решетки в момент t называется апплетом. В более строгой трактовке состояние решетки ДКА – это матрица размерностью n × m.
О клетке говорят, что она содержит или имеет соответствующее значение, либо находится или пребывает в состоянии, кодируемом данным значением. Оно можем быть булевым, целым, числом с плавающей точкой, множеством или другим объектом.
Q – конечное множество, определяющее окрестность клетки, то есть, количество k и местоположение (координаты) клеток множества Q(i), влияющих на значение данной клетки. Если j ∈ Q(i), то элемент j включается в окрестность i-ой клетки и считается ее соседом.
Для ДКА, решетка которого
представляется двумерным массивом, обычно используют
два типа окрестностей клетки: из четырех и из восьми клеток.
Окрестность из четырех
клеток (k = 4), состоящая
из ближайших недиагональных соседей клетки yi,j: yi-1,j, yi,j-1, yi,j+1, yi+1,j, называется окрестностью фон Неймана (рисунок 2.а).
Окрестность из восьми клеток
(k = 8), состоящая из восьми окружающих клетку yi,j соседей: yi-1,j-1, yi-1,j, yi-1,j+1, yi,j-1, yi,j+1, yi+1,j-1, yi+1,j, yi+1,j+1, называется окрестностью Мура (рисунок 2.б).
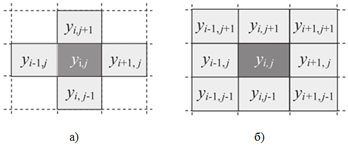
Рисунок 2 – Окрестности клетки ДКА: а) фон Неймана; б) Мура
В данной статье ограничимся рассмотрением только ДКА с окрестностью Мура.
Правила R определяют, какое значение должно содержаться в клетке в следующий момент (t+1), в зависимости от значений клеток, входящих в её окрестность Q(i), в текущий момент t, а также от значения si(t), содержащегося в ней самой в текущий момент.
Правила R для ДКА
с окрестностью Мура могут задаваться в виде 18-разрядных двоичных чисел: Rм = 000101000 011001000.
Первые девять разрядов этих чисел определяют маркеры значений суммы ![]() ,
при которых клетка, имеющая значение «1», переходит в новое состояние с этим же
значением, а следующие девять разрядов определяют маркеры значений суммы
,
при которых клетка, имеющая значение «1», переходит в новое состояние с этим же
значением, а следующие девять разрядов определяют маркеры значений суммы ![]() ,
при которых происходит «рождение» клетки, т.е. изменения ее значения с «0» на
«1». Во всех остальных случаях фиксируется «смерть» клетки, т.е. изменение ее
значения с «1» на «0» или пролонгируется ее нулевое значение.
,
при которых происходит «рождение» клетки, т.е. изменения ее значения с «0» на
«1». Во всех остальных случаях фиксируется «смерть» клетки, т.е. изменение ее
значения с «1» на «0» или пролонгируется ее нулевое значение.
Для упрощенного, но вместе с тем однозначно трактуемого варианта записи правил для ДКА, предлагается использовать обозначения вида Rм: 35/125, что эквивалентно записи Rм = 000101000 011001000.
Состояние i-ой клетки ДКА в момент (t+1) однозначно определяется функцией F от двух переменных – состояния si(t) самой клетки и суммы состояний ее ближайших соседей в предшествующий момент t:
![]() . (2)
. (2)
Для S = {0, 1} первая переменная принимает значение «0» или «1», а вторая – значения от «0» до «k», т.е. всего k+1 значение. Следовательно, исключив случай, когда не задано никаких условий «рождения» и «выживания», полное число различных вариантов задания правил перехода ДКА с заданным k составит:
NR = (2k + 1 – 1)2. (3)
Таким образом, для ДКА с
окрестностью Мура (k = 8)
число вариантов задания правил перехода будет составлять NR = (28 + 1 – 1)2 = 261121.
По своему поведению КА
делятся на четыре класса [1].
КА первого класса за конечное число шагов достигают однородного
состояния, в котором величины si(t) для всех элементов сети одинаковы и не зависят
от времени. Это однородное состояние устанавливается независимо от того, каким
было исходное состояние решетки автомата, называемое начальным (исходным) апплетом. В процессе эволюции для таких
КА полностью теряется информация о начальных условиях.
КА второго класса генерируют локализованные
простые структуры, которые могут быть стационарными или периодическими во
времени.
КА третьего и четвертого классов
обладают более сложной динамикой. Локализованное локальное возмущение порождает
процесс изменения активности, который захватывает с течением времени все
большую часть сети. Отличительной особенностью КА третьего класса является то, что статистические свойства
разворачивающегося процесса теряют зависимость от начальных условий. Тем самым
КА третьего класса обладают
«эргодическим» или «турбулентным» поведением, то есть имеют хаотическую
динамику своей эволюции.
Динамика КА четвертого класса существенно зависит от
исходного состояния решетки автомата. Подбирая определенные начальные условия,
можно генерировать самые различные последовательности сменяющих друг друга
картин. КА четвертого класса, подобно «машине Тьюринга», могут осуществлять
универсальные вычисления.
Применение дискретных отображений класса «клеточные автоматы» для создания генераторов псевдослучайных последовательностей
Дискретные отображения класса «клеточные автоматы», а именно, ДКА третьего класса, благодаря свойству нелинейности, эргодичности, турбулентноти и необратимости процесса своего развития (эволюции) по аналогии с некоторыми типами ОКА нашли применение в качестве генераторов псевдослучайных последовательностей.
В общем случае для задания генератора на ДКА необходимо выбрать (установить) тип пространства, вид решетки, тип окрестности клетки и конечное множество S возможных состояний клеток.
Как ранее упоминалось, в данной статье ограничимся рассмотрением только ДКА с окрестностью Мура. Кроме того, решетка ДКА будет «завёрнута» в тор, а S = {0, 1}. В этом случае инициализирующим вектором данных для генератора на базе ДКА являются его начальное состояние, определяемое исходным (нулевым) апплетом A0 и правилом смены внутренних состояний Rм.
Исходный апплет A0 представляет собой матрицу, в каждой ячейке которой записаны либо нули, либо единицы.
Процесс генерации псевдослучайных последовательностей посредством ДКА связан с изменением на каждой итерации по правилу Rм его внутреннего состояния, определяемого текущим апплетом At. В свою очередь каждый апплет At по определенному правилу записывается в виде последовательности n × m бит, которая конкатенируется с последовательностью бит, полученной на предыдущей (t–1) итерации.
Таким образом, результат генерации псевдослучайных последовательностей посредством ДКА можно представить в виде некоторой выборки состояний его решетки (апплетов At), разложенных в линейную последовательность бит.
Данная последовательность является результатом применения к заданному ДКА:
– функции инициализации внутреннего состояния f0, формирующей апплет A0;
– функции обновления внутреннего состояния fR, изменяющей состояния решетки по правилу Rм;
– функции вывода fv, определяющей порядок записи бит в последовательность.
С учетом изложенного можно записать:
At = fv [ fR (At-1) ]. (4)
Традиционно считается, что важными моментами при инициализации генератора на ДКА являются задание его исходного внутреннего состояния A0 и выбор правила его обновления Rм.
Генератор псевдослучайных последовательностей на базе дискретных отображений класса «клеточные автоматы» со случайными окрестностями
В работе [16] были исследованы возможности использования и пути повышения качества генераторов псевдослучайных последовательностей на базе дискретных отображений класса «клеточные автоматы». В частности были исследованы ДКА с окрестностью Мура и правилом обновления Rм: 35/125. При этом в процессе эволюции таких ДКА авторами были обнаружены «сгущения» из единичных и нулевых бит.
Одной из причин такого «сгущения» бит является то, что для двух соседних ячеек решётки ДКА 4 из 8 ячеек их окрестностей Мура являются общими.
Для устранения эффекта «сгущения» переопределим способ задания окрестности ячейки решётки ДКА следующим образом: для каждой ячейки i будет сгенерирована случайная окрестность из 8 ячеек, при чём ячейка i не может входить в свою же окрестность, и если ячейка j входит в окрестность ячейки i, то ячейка i не может входить в окрестность ячейки j.
Поскольку генерируемая числовая последовательность должна подчиняться равномерному закону распределения, соотношение «0» и «1» от итерации к итерации должно быть примерно одинаковым. Исходя из этого, вычислим минимум, максимум, среднее значение и среднеквадратическое отклонение (СКО) для модуля разности между долями «1» на соседних итерациях. При этом возьмем случайный исходный апплет A0 размером 8×8 клеток (таблица 1), в котором число «0» и «1» одинаково, и сгенерируем 10 случайных окрестностей для ДКА, а так как для случайно взятого исходного апплета не известны периоды «зацикливания»/«вырождения», вычисления произведём на протяжении 100 итераций. Результаты вычислений представлены в таблице 2.
Таблица 1 – Исходный апплет A0
|
Строка |
Столбец |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
2 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
4 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
6 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
8 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
Таблица 2 – Достигнутые результаты
|
ДКА |
Минимум |
Максимум |
Среднее |
СКО |
|
|
С окрестностью Мура |
0,000 |
0,281 |
0,084844 |
0,059958 |
|
|
Со случайной окрестностью |
1 |
0,000 |
0,266 |
0,079063 |
0,055013 |
|
2 |
0,000 |
0,250 |
0,087031 |
0,058013 |
|
|
3 |
0,000 |
0,219 |
0,066563 |
0,051188 |
|
|
4 |
0,000 |
0,234 |
0,071563 |
0,051405 |
|
|
5 |
0,000 |
0,266 |
0,077500 |
0,057151 |
|
|
6 |
0,000 |
0,250 |
0,078750 |
0,058710 |
|
|
7 |
0,000 |
0,391 |
0,075938 |
0,072215 |
|
|
8 |
0,000 |
0,219 |
0,067188 |
0,054374 |
|
|
9 |
0,000 |
0,391 |
0,083594 |
0,079407 |
|
|
10 |
0,000 |
0,297 |
0,089844 |
0,065453 |
|
На основании данных таблицы 2 можно сделать вывод о том, что в среднем на 8,42% для ДКА со случайной окрестностью динамика соотношения «0» и «1» равномернее, чем для ДКА с окрестностью Мура.
Все эксперименты проводились с использованием программы, написанной на языке программирования Python. Листинг программы:
#!/usr/bin/env
python
import
os
import
random
import
math
def
mean(vals):
result = 0
if len(vals):
result = sum(vals) / len(vals)
return result
def
variance(vals):
vals_mean = mean(vals)
result = 0
for val in vals:
result += (val - vals_mean) * (val -
vals_mean)
result /= len(vals)
return result
def
std_dev(vals):
return math.sqrt(variance(vals))
class
CA(object):
rows = 0
cols = 0
R1 = []
R0 = []
cur = {}
def _get_p(self):
val = 0
for i in range(0, self.rows):
for j in range(0, self.cols):
val += self.cur[i][j]
return float(val)/(self.rows *
self.cols)
def _get_s(self, i, j):
val = 0
for n in range(-1, 2):
i_n = i + n
if i_n < 0:
i_n += self.rows
elif i_n >= self.rows:
i_n -= self.rows
for m in range(-1, 2):
j_m = j + m
if j_m < 0:
j_m += self.cols
elif j_m >= self.cols:
j_m -= self.cols
if n or m:
val += self.cur[i_n][j_m]
return val
def _print(self):
val = "\n"
for i in range(0, self.rows):
for j in range(0, self.cols):
val += str(self.cur[i][j])
val += "\n"
print val
def __str__(self):
val = ""
for i in range(0, self.rows):
for j in range(0, self.cols):
val += str(self.cur[i][j])
return val
def __init__(self, rows, cols, R1, R0,
initial=None):
super(CA, self).__init__()
assert rows > 0 and cols > 0
self.rows = rows
self.cols = cols
self.R1 = R1
self.R0 = R0
self.cur = {}
if initial is None:
init = True
while init:
for i in range(0, self.rows):
self.cur[i] = {}
for j in range(0,
self.cols):
self.cur[i][j] =
random.randrange(0, 2)
init = self._get_p() != 0.5
else:
assert len(initial) == self.rows *
self.cols
for i in range(0, self.rows):
self.cur[i] = {}
for j in range(0, self.cols):
self.cur[i][j] =
int(initial[self.rows * i + j])
assert self.cur[i][j] in
[0, 1]
def _func_0(self, i, j):
if self._get_s(i, j) in self.R0:
return 1
else:
return 0
def _func_1(self, i, j):
if self._get_s(i, j) in self.R1:
return 1
else:
return 0
def _run(self, time):
stat_val = [self._get_p()]
stat_dif = []
for cur_time in range(0, time):
next = {}
for i in range(0, self.rows):
next[i] = {}
for j in range(0, self.cols):
if self.cur[i][j]:
next[i][j] = self._func_1(i,
j)
else:
next[i][j] =
self._func_0(i, j)
self.cur = next
stat_val.append(self._get_p())
stat_dif.append(abs(stat_val[-1] -
stat_val[-2]))
print stat_val
print min(stat_dif), max(stat_dif),
mean(stat_dif), std_dev(stat_dif)
class
CAM(CA):
neighbors = {}
def _get_s(self, i, j):
val = 0
for v in self.neighbors[i][j]:
val += self.cur[v[0]][v[1]]
return val
def _print(self):
super(CAM, self)._print()
for i in range(0, self.rows):
for j in range(0, self.cols):
print (i, j),
self.neighbors[i][j]
print
def __init__(self, rows, cols, R1, R0, initial=None):
super(CAM, self).__init__(rows, cols,
R1, R0, initial)
self.neighbors = {}
for i in range(0, self.rows):
self.neighbors[i] = {}
for j in range(0, self.cols):
self.neighbors[i][j] = []
s = self.rows * self.cols
for n in range(0, 8):
for i in range(0, self.rows):
for j in range(0, self.cols):
init = True
while init:
v = random.randrange(0,
s)
v = (v / self.rows, v %
self.rows)
if v[0] == i and v[1]
== j:
continue
if v not in
self.neighbors[i][j]:
init = False
for w in
self.neighbors[v[0]][v[1]]:
if (i, j) in
self.neighbors[w[0]][w[1]]:
init = True
if not init:
self.neighbors[i][j].append(v)
if
__name__ == "__main__":
t = 100
ca = CA(8, 8, [3, 5], [1, 2, 5])
initial = str(ca)
ca._print()
ca._run(t)
ca._print()
for n in range(0, 10):
print "#%s" % n
cam = CAM(ca.rows, ca.cols, ca.R1,
ca.R0, initial)
cam._run(t)
cam._print()
Заключение
В работе предложен новый вид окрестности для ячеек решётки ДКА, позволяющий добиться более равномерной динамики изменения соотношения «0» и «1» в процессе его эволюции.
Список литературы
1. S. Wolfram. Random Sequences Generation by Cellular Automata. Advances in Applied Mathematics, vol.7, 1986. pp.123-169
2. M. Sipper and M. Tomassini: Generating parallel random number generators by cellular programming, Int. J. Mod. Phys. vol. 7, pp. 181-190, 1996
3. M. Tomassini and M. Perrenoud: Nonuniform cellular automata for cryptography,
Complex Systems, vol. 12, 2000. pp. 71-81
4. M. Tomassini et al.: Generating high-quality random numbers in parallel by
cellular automata, Future Generation Computer Systems, vol. 16, 1999. pp.
291-305.
5. P. D. Hortensius et al.: Cellular
automata-based pseudorandom number generators for built-in selftest, IEEE Transactions on Computer-aided
Design, vol. 8, 1989. pp. 842–859
6. P. D. Hortensius, R. D. McLeod, and
H. C. Card, «Parallel number generation for VLSI systems using cellular automata» IEEE Transactions on Computers, vol.
38, no. 10, October 1989. pp. 1466-1473
7. Асосков Г.А., Тихоненко Е.А. Новый генератор случайных чисел на базе двумерного клеточного автомата. Матем. моделирование, 8:12 (1996). с. 77-84.
8. M. Sipper and M. Tomassini,
«Generating parallel random number generators by cellular programming», International Journal of Modern Physics
C, vol. 7, no. 2, 1996. pp. 181-190
9. B. Shackleford, M. Tanaka, R. J. Carter, G. Snider, «FPGA Implementation of Neighborhood-of-Four Cellular Automata Random Number Generators», Hewlett-Packard Laboratories, 1501 Page Mill Rd. Palo Alto, CA 94304 U.S.A.
10. D. R. Chowdhury, I. Sengupta, and P.
P. Chaudhuri, «A class of two-dimensional cellular automata and their applications in random pattern testing», Journal
of Electronic Testing, vol. 5, 1994. pp. 67-82
11. F. James. A Review of Pseudorandom Number Generators. Computer Physics
Communications, vol. 60, 1990. pp.329-344
12. M. Tomassini, M. Sipper, and M.
Perrenoud, «On the generation of high-quality random numbers by two-dimensional cellular automata», IEEE Transactions on
Computers, vol. 49, October 2000. pp. 1146-1151
13. Song-Ju Kim, Ken Umeno. Randomness Evaluation and Hardware Implementation of
Nonadditive CA-Based Stream Cipher, J Signal Process, vol. 9, No.1, 2005. pp.
71-77
14. S. Wolfram. Statistical Mechanics of Cellular Automata. Rev. Modern Phys, vol. 55, 1983.
15. T. Toffoli, N. Margolus. Cellular Automata Machines: A New Environment For Modelling. MIT Press, Cambridge, Mass., 1987.
16. Смуров С.В., Нижниковский А.В., Буланов Д.В. Теория, применение и пути повышения качества генераторов псевдослучайных последовательностей на основе формализованных моделей дискретных отображений класса «клеточные автоматы // «Известия института инженерной физики». – 2011. ‑ №2. – с. 2-19.