SOLVING THE SECOND ORDER NON-CONSTANT
COEFFICIENT DIFFERENTIAL EQUATIONS
Fazilova F.B., Abdyla R., Zhunisbekova D.А.
M. Auezov
South-Kazakhstan state university
The theory of
the differential equations belongs to number of the relatively young and
roughly developing sections of the theory of the ordinary differential
equations. There are a number of monographs, entirely or partially devoted to
various aspects of this theory. We will specify, first of all, Myshkis A.D.
monographs, Elsgoltsa L.E., Krasovsky N.N., Pinni E., Bellman R., Cook K.L.
Consider the
differential equation,
.
Assume
that 
and 
are a fundamental set of solutions for
.
Then a
particular solution to the nonhomogeneous differential equation is,
.
Depending
on the person and the problem, some will find the formula easier to memorize
and use, while others will find the process used to get the formula
easier. The examples in this section will be done using the formula.
Before
proceeding with a couple of examples let’s first address the issues involving
the constants of integration that will arise out of the integrals. Putting
in the constants of integration will give the following:
=
.
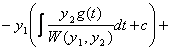
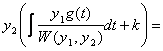
The
final quantity in the parenthesis is nothing more than the complementary
solution with c1 = -c and c2 =
k and we know that if we plug this into the differential equation it
will simplify out to zero since it is the solution to the homogeneous
differential equation. In other words, these terms add nothing to the
particular solution and so we will go ahead and assume that c =
0 and k =
One
final note before we proceed with examples. Do not worry about which of
your two solutions in the complementary solution is and which one is 
. It doesn’t matter. You
will get the same answer no matter which one you choose to be and which one you choose to
be .
For example, let’s find a general solution to the following
differential equation
.
We first need
the complementary solution for this differential equation. We’ll leave it
to you to verify that the complementary solution is,
.
So, we have 
, 
.
The Wronskian of
these two functions is
.
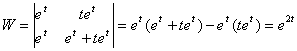The particular
solution is then,
.
The general
solution is,
.
This
method can also be used on non-constant coefficient differential equations,
provided we know a fundamental set of solutions for the associated homogeneous
differential equation.
Let’s find the general solution to 
given that , 
, form a fundamental set of solutions for the homogeneous
differential equation.
As with the
first example, we first need to divide out by a t
.
The Wronskian
for the fundamental set of solutions is
.
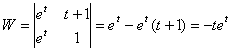The particular solution is
.
The general
solution for this differential equation is
.
The
solution can be simplified down somewhat if we do the following
.
Now,
since 
is an unknown constant
subtracting 2 from it won’t change that fact. So we can just write
the 
as and be done with it.
Literature
1.Pinni
E. Ordinary differential-difference equations. - M.: SILT, 1961. – 248 pp.
2.Norkin
S. B. The differential equations of the second order with the late argument.
Some questions of the theory of
fluctuations of systems with delay. - M.: Science, 1965. – 354 pp.