К. ф.-м. н. Махина Н.М.

Брянский государственный университет им. ак. И.Г. Петровского, Россия

Некоторые замечания к вопросам оценки

конформно отображающей функции

в областях комплексной плоскости

Возможность использовать те или иные оценки конформно отображающей функции является классической во многих задачах комплексного анализа (см. [1]-[3])).

В данной заметке мы обобщим некоторые известные и новые факты, касающиеся оценок вышеуказанной функции в областях комплексной плоскости с различными границами.

Обозначим , – некоторая односвязная область на комплексной плоскости ; функция конформно отображает на , – обратная функция для ; – расстояние от точки до границы области .

Для произвольной области комплексной плоскости хорошо известно двойное неравенство, которое выводится из теоремы Кёбе (см. [4, с. 51])

.

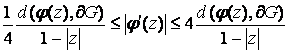Возникает вопрос: можно ли уточнить данные оценки или вывести другие для некоторых областей?

Пусть (С) – класс односвязных областей на комплексной плоскости, граница каждой из которых состоит из конечного числа гладких дуг , образующих между собой в точках стыка положительные внутренние углы (см. [5]).

Приведем оценки конформно отображающей функции в соответствующих пространствах областей с границей класса (C) при всех (см. [6]).

Теорема 1. Пусть , – функция Римана, отображающая S на G, причем , , . Тогда при , , справедливы оценки

1) При

,

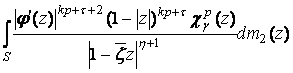
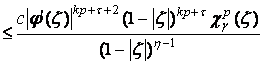где , , , , ,

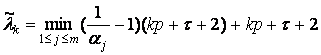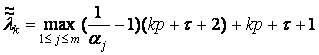2) При

,

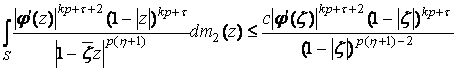где , .

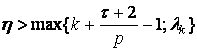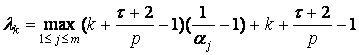Напомним, что область G принадлежит классу областей с асимптотически конформной границей, если

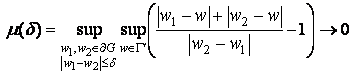при

где – кратчайшая дуга кривой, соединяющей точки .

Отметим, что если – функция Римана, конформно отображающая единичный круг на область с асимптотически конформной границей, то (см. [7]). Как известно (см., например, [8]), если , то .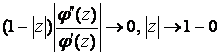

Оценки конформно отображающей функции в классе областей с границами класса типа Лаврентьева, то есть кривых таких, что , где , – произвольные точки на кривой, – длина кратчайшей дуги кривой, соединяющей точки (см., например, [4]), выглядят, например, так

Теорема 2. Пусть – односвязная ограниченная область, , функция конформно отображает на , причем – некоторая точка из , . Пусть также , , Тогда

1) Если то справедлива оценка

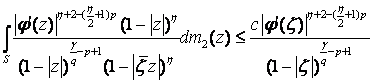
2) Если , то справедлива оценка

.

Аналог подобной теоремы использовался в работах [2], [3].

Литература:

1. Ткаченко Н.М. Об оценках модуля производной аналитической в угловой области функции // Вестник ИжГТУ им. М.Т. Калашникова. 2008. № 1. С. 96-98.

2. Tkachenko N.M., Shamoyan F.A. The Hardy-Littlewood theorem and the operator of harmonic conjugate in some classes of simply connected domains with rectifiable boundary // Журнал математической физики, анализа, геометрии. – 2009. Т. 5. № 2. С. 192-210.

3. Махина Н.М. Базисы в весовых пространствах функций, аналитических в областях со спрямляемой границей // Вестник Брянского государственного университета: Естественные и точные науки. 2013. №4. С. 27-32.

4. Голузин Г.М. Геометрическая теория функций комплексного переменного. – М.: Наука, 1966.

5. Дзядык В.К. Введение в теорию равномерного приближения функций полиномами. – М.: Наука, 1977.

6. Ткаченко Н.М. Весовые Lp-оценки аналитических и гармонических функций в односвязных областях комплексной плоскости // диссертация на соискание ученой степени кандидата физико-математических наук / Саратовский государственный университет им. Н.Г. Чернышевского. Брянск, 2009.

7. Pommerenke Ch. On univalent functions, Bloch functions and VMOA / Ch. Pommerenke // Math. An. 1978. V. 236. P. 199-208.

8. Гарнетт Дж. Ограниченные аналитические функции. – М.: Мир, 1984.