Ендураева Н.А.
Релаксационный
метод адаптации модели сети нефтепроводов
Самарский
Государственный Технический Университет, г. Самара
Ключевые слова: наземное обустройство, перспективное планирование, гидравлический расчет, адаптация модели.
Аннотация
В работе рассматривается задача настройки теоретической гидравлической
модели трубопроводной сети на воспроизведение фактических показателей расхода
жидкости, давления и температуры с целью обеспечения физичности и надёжности
результатов расчёта.
Отмечается, что технологические мероприятия по системам трубопроводов
принимаются на основании гидравлических расчётов. От корректности каждого
расчёта напрямую зависит эффективность принимаемых решений.
Вводится понятие адаптации как процесса настройки теоретической модели
для наиболее точного воспроизведения реальности. Отмечается высокая
трудоёмкость этого процесса, которая расчёт с увеличением масштаба модели и
степени неопределённости её параметров. Предлагается автоматизировать адаптацию
с помощью математического метода релаксации.
Введение
Технологические
решения в нефтегазовой отрасли принимаются на основании оценки их технико-экономической
целесообразности. Подобная оценка делается с применением современных методик,
алгоритмов и программных средств [1-2]. Не составляют исключения и
гидравлические расчёты, связанные с анализом распределения жидкости и давления
в системах трубопроводов и технологического оборудования.
Эти
расчёты чрезвычайно важны как при планировании ввода новых мощностей, так и при
разработке программ реинжиниринговых мероприятий на зрелых активах, в связи с
тем, что от корректности гидравлического расчёта напрямую зависит эффективность
принимаемых решений и, соответственно, надёжность системы трубопроводов.
Некорректная оценка этих показателей может привести к авариям, значительным
потерям продукции и, как следствие, экономическим издержкам.
Релаксационный метод адаптации
гидравлической модели
На
рисунке 1 представлен условный пример – перспективные уровни добычи жидкости с
куста скважин (чёрные столбцы), а так же профиль давления (чёрная линия –
замер; красная – расчёт). На начальный период горизонта планирования (2016 год)
расчётное давление (15 атм) превышает замерное на 5 атм. Предполагается
троекратный рост добычи жидкости в течение 5 лет. Для наглядности примера
предполагается пропорциональный (троекратный) рост давления. Показано, что
расчётное (прогнозное) давление на 2021 год (30 атм) покажет достаточность
пропускной способности системы сбора, в то время как фактическое давление (45
атм) будет недопустимым с точки зрения надёжности и приведёт к невозможности выполнения
ожидаемых уровней добычи. То есть модель, показывающая незначительное
отклонение от фактических замеров «сегодня», может привести к ощутимым ошибкам
в перспективных планах.
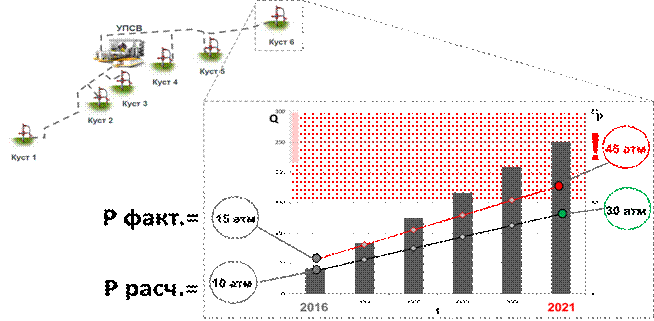
Рис. 1. Условный пример для иллюстрации
актуальности рассматриваемого вопроса.
Основная
задача теоретической гидравлической модели – как можно более точное
воспроизведение характеристик поведения реальной системы трубопроводов. Поэтому
важно настроить модель так, чтобы результаты её расчётов имели значительную
степень надёжности. Процесс настройки модели для более точного воспроизведения
реальности называется адаптацией.
Адаптация
модели всегда связана с неопределённостью, т.е потенциал для адаптации
составляют неизвестность или ненулевой допустимый интервал значений для какого-либо
параметра. Технически адаптация – это вариация параметров модели, имеющих
диапазон неопределённости, и уточнение их значений для минимизации ошибки между
результатами модели и целевыми значениями, в качестве которых зачастую
выступают замеры.
По
трудоёмкости адаптация занимает основную часть гидравлического расчёта. Это
связано с многопараметричностью гидравлической модели, которая приводит к
формированию достаточно обширной области поиска решения, размерность которой
кратна количеству параметров с ненулевым диапазоном неопределённости. Это
исключает возможность решения задачи простым перебором. Характер расширения
области поиска решения с ростом количества неопределённых параметров показан на рисунке 2. Кроме того,
ресурсы, требующиеся для выполнения адаптации, растут с увеличением масштаба
модели и диапазона неопределённости каждого параметра. В связи с этим,
актуальность задачи данного исследования связана не только с качеством
технологических расчётов, но и с экономической целесообразностью, обусловленной
экономией трудозатрат.
в б а
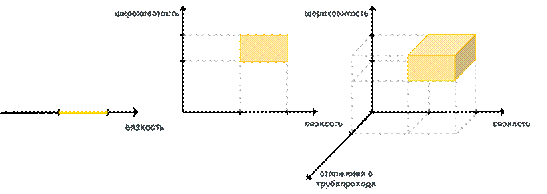
Рис. 2. Область поиска решения для случаев: а).
один параметр, имеет диапазон неопределенности; б). два параметра, имеющие
диапазон неопределенности; в). три параметра, имеющие диапазон неопределенности
В
рамках данного исследования была разработана методика автоматической адаптации
гидравлической модели системы трубопроводов при заданных диапазонах неопределённости
её параметров.
В
основе предлагаемого метода адаптации лежит классический математический метод
релаксации. На каждой итерации варьируется отдельный параметр при фиксированных
прочих. Цикл повторяется до достижения целевого результата, исключая ошибку
взаимного влияния параметров (рис. 3). Более подробно о математическом методе
релаксации можно узнать из источника [3].

Рис. 3. Математическая формализация предлагаемой
методики.
Перечень
параметров адаптации, их ранжирование (по степени влияния на результат, по
степени неопределенности) выполняется экспертом. На каждой итерации неопределенность
модели разрешается, вследствие чего повышается эффективность принимаемых технологических
решений и, соответственно, надёжность системы трубопроводов.
Заключение
Разработанная
методика реализована и апробируется в рамках выполнения гидравлических расчетов
для АО «Самаранефтегаз». Использование методики позволяет повысить
качество моделирования гидравлических сетей, а также сократить трудозатраты на
выполнение гидравлических расчетов.
Предлагаемый
механизм является интегрируемым инструментом, совместимым с любым гидравлическим
симулятором, имеющим программный интерфейс доступа.
Список использованных источников
1.
Beggs, D.H., Brill, J.P. «A Study of Two-Phase Flow in Inclined
Pipes», J. Petroleum Technology. – V.25, №5. – 1973;
2.
Маркман
П.Г., Коркин Р.В. Трубопроводный транспорт скважинной продукции //Томск: ТПУ,
2009. – 235 с.;
3.
Воеводин
В.В. Вычислительные основы линейной алгебры //Москва: Наука, 1977. – 307 с.