Рахимжанова А.Ж.

Казахский Национальный Университет имени аль Фараби, Казахстан

Казахская головная архитектурно-строительная академия,Казахстан

Исследование нелинейных колебаний неуравновешенной центрифуги

В настоящее время весьма активно изучается и вызывает большой интерес к исследованию роторных систем с полостями, частично заполненными жидкостями, так как они занимают особое место в структурах высокоскоростных машин и механизмов нового поколения. Роторные машины являются одной из энергетических основ существования современного машиностроения (турбокомпрессоры, центробежные насосы, электрические и газотурбинные двигатели и др., повсеместно используемые в энергетике, в химической, текстильной промышленности, в транспорте и строительстве и т.д.). И обеспечение устойчивой и безаварийной работы роторных систем, применяемых во многих отраслях машиностроения остается одним из наиболее сложных обьектов исследования механики. Поэтому их развитие, разработка современных моделей и разновидностей, эффективных методов анализа и оценки технического состояния привлекает внимание многих ученых[1-3, др.].

Рассматриваемая постановка задачи в данной работе является намного шире и решение задачи усложняется тем, что для построения динамической модели системы «ротор-жидкость-фундамент», наиболее полно отражающей ее реальное состояние, учитываются такие факторы как колебания фундамента, колебания жидкости, упругие характеристики опоры подшипников качения, статическая и динамическая неуравновешенность ротора, внешнее и внутреннее трение вала.

В задачах рассматривается неуравновешенная центрифуга с высотой , радиусам, массой и заполнена несколькими вязкими жидкостями (количество жидкостей равно n). Основная модель получена на оснований уравнений Лагранжа II рода. Для решения данной задачи требуется исследование отдельно собственных колебаний и вынужденных колебаний, так как движения роторной системы с жидкостью описываются нелинейными дифференциальными уравнениями. Вынужденные колебания центрифуги и ее фундамента обусловлены неуравновешенностью центрифуги, поэтому они имеет вид

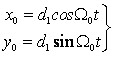
(1)

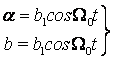(2)

Подставляя (1) и (2) в уравнения движения жидкости и решая их убедимся, что компоненты скорости частицы жидкости функции и переменная часть давления при вынужденном колебаний центрифуги и ее фундамента не зависят от времени и равны нулю в любом слое жидкостей, тогда функция с учетом (1), (2) примет вид

(3)

Подставляя выражение (3) на формулы силы реакции жидкостей и их момента относительно осей и получим их в комплексной форме(рис.1)

(4)

(5)

где 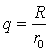–степень заполнения ротора жидкостью, – масса -ого слоя жидкости, необходимая для полного заполнения полости центрифуги.

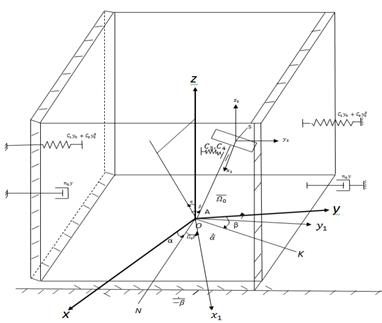
Рисунок1. Система координат определяющая движения жидкости роторных систем

Тогда подставляя (1), (2), (4) и (5) в уравнения движения центрифуги и ее фундамента получим

(6)

(7)

Упрощая системы получим полином 9-ой степени относительно амплитуды вынужденных колебаний фундамента .

(8)

Решая уравнение (14) с помощью стандартной подпрограммы на ЭВМ можно найти 9 безразмерных значений амплитуды вынужденных колебаний фундамента . А из формулы (13) находим амплитуду вынужденных угловых колебаний центрифуги . Амплитуды колебаний центрифуги и ее фундамента должна быть действительным и положительным. Поэтому для каждого значения угловой скорости центрифуги , берется только те значения, которые являются действительными и положительными.

Для определения зависимости амплитуды вынужденных колебаний и от угловой скорости , когда присутствует внешние демпфирования и используется метод последовательных приближений (метод итерации). Плавно изменяя угловой скорости центрифуги в широких пределах при вариации параметров роторной системы ) можно найти зависимостей амплитуд вынужденных колебаний центрифуги и ее фундамента.

Как известно существенной особенностью нелинейной системы является возможность появления нескольких периодических режимов при изменении частоты колебания системы, т.е. угловой скорости центрифуги .

Когда известны амплитуды вынужденных колебаний системы и из формулы (8) находим сдвиг фазы вынужденных колебаний центрифуги и ее фундамента и .

ЛИТЕРАТУРА

1 Arturas Tadzijeva, Vitautas Barzdaitis. Vertical versus horizontal rotors dynamics and diagnostics//11th International Conference on Vibration problems. Lisbon, Portugal, 9-12 September 2013.

2 Xuening Zhang, Qinkai Han, Zhike Peng, Fulei Chu. A new nonlinear dynamic model of the rotor-bearing system considering preload and varying contact angle of bearing// Commun nonlinear simulate 22(2015) 821-841.

3 Dimarogonas A.D., Paipetis S.A., ChondrosTh.G. Analytical Methods in Rotor Dinamics.Second Edition.20\

4 Sundararajan P., Noah S. An algorithm for response and stability of large order non-linear systems – application to rotor systems // Journal of Sound and Vibration. – 1998. – Vol.214. – P. 695-723.

5 Zhu Changsheng. Stability behaviour of an isotropic rotor system anisotropically mounted and partially filled with inviscous fluid // Proceedings of IMAC-19: A Conference on Structural Dynamics. – Kissimmee, Fla. – Febr. 5-8, 2001. – P. 1278-1283.

6 Дерендяев Н.В., Солдатов И.Н. Устойчивость стационарных движений роторной системы с жидкостью в рамках дискретной модели // ПММ. –2004. – Т.68, № 6. – С. 984-993.

7 Дерендяев Н.В. Динамика роторных систем, содержащих жидкость // Вестник ННГУ. Серия механика. – 2001. – Вып.1(3). – С. 26-28.

8 Derendyayev N.V., Soldatov I.N., Vostrukhov A.V. Stability and Andronov-Hopf bifurcation of steady-state motion of rotor system partly filled with liquid: continuous and discrete models // Trans. ASME. Journal of Applied Mechanics. – 2006. – Vol. 73, № 4. – P. 580-589.

9 Feng N., Hahn E. Experimental identification of the pedestal in a rotor-bearing-pedestal system // Proc. 5th IFToMM International Conference on Rotor Dynamics. – Darmstadt, Germany, 1998. – P. 734-745.