Сланбекова А.Е., Каменова Ш.К., Рахимжанова С.Е

Е.А. Бөкетов атындағы Қарағанды мемлекеттік университеті, №22 орта мектеп-интернат, Қазақстан

Мазмұнды логикалық есептерді шешудің жолдары

Біздің заманымызда қоғамды дамыту үшін жеке тұлғаның алдында тұрған негізгі міндеттердің бірі - қоғам құруға өзінің бар мүмкіндігін жұмсайтын шығармашыл, қабілетті маман болу. Мазмұнды есептерді шығару адамдарды алғырлыққа, ой ұшқырлыққа, логикасын жетілдіріп, тез ойлауға, тапқырлыққа тәрбиелейді. Сондықтан да, әрбір оқушы математикалық сауатты болу үшін мынадай мақсаттарды жүзеге асыру керек: ақыл - ойды дамыту, математикалық іс-әрекеттің сипатына сай ойлауды қалыптастыру, қоғамдық өмір практикасына қажетті математикалық ойлауды қалыптастыру, математикалық білімді игеру мақсатында практикада қолдануды, болмысты, табиғат пен қоғамды тануға қажет математикалық мазмұндай білу, алдына қойылған сұрауға немесе есепті шығаруға тиімді (жылдам, сенімді және дұрыс) жауап беруге дағдылану, ұмтылу.

Арнайы формуланы қолдануға келмейтін әрқайсысына өзінше талдау жасауды қажет ететін есептерді логикалық есептер деп атаймыз. Мазмұнды логикалық есептерді шығару үшін шешуді жүзеге асыруда мүмкіндіктерді есептеудің тәсілдерін көрсеткен жөн.

Мысалыға «Алты қанат киіз үйге екі мысық келіп кірді де, бірінші керегенің түбіне екеуі балалап, әрқайсасы алтыдан балалады. Олардың бәріде мысық болып өсті де, тағыда алты - алтыдан балалады, т.с.с. осылайша әр керегенің түбіне барып балалап шықты». Сонда киіз үйден неше мысық өсіп шығады?

Бірінші есептің шартымен танысып, оны элементар шарттарға ажыратып, қандай талаптар қойылғанын анықтап есепті талдаймыз, яғни алты қанат киіз үй туралы түсінік, мысықтардың өсімталдығы туралы, әр кереге түбіне әрқайсысы алтыдан мысық шығаратыны туралы түсінік беру. Екінші есепті схема сурет түрінде жазу. Үшінші шығару тәсілін іздеу – әр керегенің түбіне 6-дан балалайтын болғандықтан, әр керегедегі мысықтар санын 6-ға көбейту. Төртінші табылған тәсіл бойынша есепті шығару: әр керегедегі мысық саны: 12+72+432+2592+15552+93312=111972. Бесінші есептің нәтижесін тексеру:

2·6=12 432·6=2592

12·6=72 2592·6=15552

72·6=432 15552·6=93312

Алтыншы есепті зерттеу: әр керегеде мысықтар саны өсіп 6 есеге көбейіп отырады. Жетінші жауабын тұжырымдау керек: алты қанат киіз үйден барлығы 111972 мысық өсіп шығады.

Мазмұнды есептер шығаруда теңдеу құру арқылы шығаратын есептерді шығару алгоритмін мысал арқылы орындайық. Тендеулер жүйесін құру тақырыбына: «Қаз бен түлкі» ертегісін оқи отырып, мына теңдеуді шешеміз:

«Түлкісін аярлыққа бермейтін дес,

Көрейін сенде қанша ақыл мен ес.

Балапан, көжек санын өзің тапшы

Аяқтарды 94, басы 35»

Бірінші есептің мәтінін түсіну. Түлкінің айлакерлігі, қаздың ақылдылығы, балапанда - 2 аяқ, көжекте - 4 аяқ.

Екінші теңдеу құру: Балапан саны – х, көжек саны – у, балапанда 2 аяқ – 2х, көжекте 4 аяқ – 4х.

Сонда Теңдеулер жүйесі шығады.

Үшінші теңдеулер жүйесін шешу.

Төртінші теңдеудің шешімдерін зерттеу: Балапан – 23, көжек – 12, бастарының саны 23 + 12 = 35, аяқтарының саны 2·23+4·12=46+48=94

Бесінші есептің жауабы: 23 балапан, 12 көжек.

Келесі қызықты, әрі тосын жағдайларға бірнеше мысал келтірейік.

Бірінші есеп төмендегідей қасиеттері бар екі таңбалы санды табыңдар.

Ондық цифры бірлік цифрынан 4-ке кем. Егер сол цифрлармен, бірақ керісінше жазылған саннан ізделінді санды шегерсе, онда 27 шығады. Ондықтар цифрын х арқылы, ал бірліктер цифрын у арқылы белгілеп, бұл есеп үшін мына теңдеулер системасын оп-оңай құрамыз:

х-тің бірінші теңдеудегі мәнін оның екінші теңдеудегі орнына қойып, мынаны табамыз: 10y + у−4−[10 у−4) y]=27, осыны түрлендіргенімізде мынау шығады: 36 = 27.

Белгісіздердің мәндері анықталмағанымен, оның есесіне біз 36 = 27. болатынын білдік. Бұл не деген сөз? Бұл - есепте қойылған шартты қанағаттандыратын екі таңбалы сан жоқ және құрылған теңдеулер бір-біріне қайшы - деген сөз. Шынында да: бірінші теңдеудің екі жағын 9-ға көбейтіп, одан біз мынаны табамыз: 9y - 9x = 36, ал екінші теңдеуден (жақшаларды ашып, ұқсас мүшелерді біріктіргеннен соң) мынау шығады: 9y - 9x = 27.

Бір ғана 9y - 9x шамасы бірінші теңдеу бойынша 36-ға тең, ал екіншісі бойынша 27-ге тең. Бұлай болуы мүмкін емес, себебі 36≠27.

Төмендегі теңдеулер системасын шешкенде де осындай қателік кездеседі:

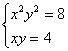
Бірінші теңдеуді екіншіге бөліп, мынаны табамыз: ху = 2, осы теңдеуді екінші теңдеумен салыстырсақ, мынаны байқаймыз:

яғни 4 = 2. Бұл теңдеулер системасын қанағаттандыратын сан жоқ. (Осы қарастырылып өткен теңдеулер системасы үйлесімсіз деп аталады.)

Екінші есеп егер алдыңғы есептің шартын біраз өзгертсек, біз басқа түрдегі тосын жағдайға тап боламыз. Атап айтқанда, ондық цифр бірлік цифрдан 4-ке емес, 3-ке кем деп есептейміз, ал есептің өзге шартын бұрынғысын-ша қалдырамыз. Бұл қандай сан?

Теңдеу құрамыз. Егер ондық цифрды х арқылы белгілесек, онда бірлік цифр х + 3 өрнегі арқылы өрнектеледі. Есепті алгебра тіліне аударып, мына теңдеуді шығарып аламыз: 10(х + 3) + х− [10х + (х+3)] = 27.

Енді ықшамдасақ, мына теңдік шығады: 27 = 27.

Бұл теңдік сөзсіз тура, бірақ ол х-тің мәні туралы ештеңе білдірмейді. Бұл есептің талабын қанағаттандыратын сан жоқ деген сез бе? Керісінше, бұл біз құрастырған теңдеудің теңбе-теңдік екенін білдіреді, яғни ол теңдеу х белгісіздің кез келген мәнінде тура. Шынында, бірлік цифры ондық цифрынан 3-ке артық болатын кез келген екі таңбалы санның осы есепте көрсетілгендей қасиеті бар екеніне оп-оңай көз жеткізуге

14 + 27 = 41, 47 + 27 = 74,

25 + 27 = 52, 58 + 27 = 85,

36+27 = 63, 69 + 27=96.

Үшінші есеп төмендегідей қасиеттері бар үш таңбалы санды табыңдар:

1 ондық цифры 7;

2 жүздік цифры бірлік цифрынан 4-ке кем;

3 егер осы санның цифрлары кері ретпен орналастырылса, онда жаңа сан ізделіп отырған саннан 396-ға артық болады. Бірлік цифрын х арқылы белгілеп, теңдеу құрамыз: 100х + 70 + х−4−[100 (х−4) + 70 + х] = 396.

Бұл теңдеуді ықшамдағаннан соң, мынадай теңдік шығады: 396 = 396.

Бұл бірінші цифры үшінші цифрынан 4-ке кем кез келген үш таңбалы сан цифрларын кері ретпен орналастырғанда 396-ға артатынын білдіреді.

Қорыта айтқанда, мазмұнды логикалық есептерді шығарудағы қиыншылықтар, олардың алатын орны мен мүмкіндіктерді есептеудің тәсілдері қарастырылды. Мұндағы мақсат – әр баланың өзінің білім деңгейін көтеру, сабаққа деген қызығушылығын арттыру, іздену. Бұны іске асырудың бір жолы қызықтыратын тапсырмалар таңдай білу.

Математиканың сан алуан сырын, сандар әлемінің қызық құбылысын, ойлау элементтерімен өрнектеген зерттеу жұмыстары балалардың қарапайымнан басталып, біртіндеп қиындап, танымдық қызметін белсендіруге, білгенін тереңдетіп, жаңа іс-қимылға жетелейді. Зерттеу жұмыстарын жүргізу барысындағы мазмұнды логикалық есептер балаларды тез ойлай білуге, ой ұшқырлығын тереңдеуге, кең ауқымды есептерді шешуге және математикалық ойлауды қалыптастырады. Сондықтан, бұл шығармашылық жұмыс келешекте оқушыға өз білімдерін тереңдетуге көмектеседі деп сенеміз.

Әдебиеттер тізімі:

1 Тарасов Л.В. Элементы и приложения теории вероятностей в школе. – М, 1996 г.

2 П.Я.Депман, Н.Я.Виленкин. За старницами учебника математики. М:» Просвещение» 1989 г.

3 Ж.А.Елшебай «Зерек» Алматы 1991 ж.