Физика /1.Теоретическая физика

Уколов Д.В.

Государственный морской университет имени адмирала Ф.Ф.Ушакова ,

Россия

Комбинационное рассеивание света

Комбинационное рассеивание света существует двух видов: простое комбинационное рассеивание света и вынужденное комбинационное рассеивание света.

Рассмотрим простое комбинационное рассеивание света. Из истории открытия простого комбинационного рассеивания света следует, что в феврале 1928 года в Индии ученые Раман и Кришнан проводили эксперимент, в котором облучали жидкость пучком света и наблюдали за линиями спектра излучения. В результате эксперимента ученые регистрировали новые спектральные линии излучения, тем самым открыв комбинационное рассеивание света. В этом же году, в том же месяце в МГУ, в Москве ученые Ландсберг и Мандельштам проводили похожий эксперимент, в котором облучали пучком света кристаллы и так же регистрировали новые линии спектра излучения. Индийские ученые опубликовали результаты своего эксперимента через несколько дней, а российские ученые только лишь через несколько месяцев. Позже оказалось, что российские ученые открыли данный эффект 21 февраля 1928 года, а индийские ― 28 февраля 1928 года. Но к тому времени эффект уже был назван «эффектом Рамана», и нобелевскую премию получил только Раман [2,3].

Простое комбинационное рассеивание света определяется как: неупругое столкновение между частицами света (фотонами) и молекулами вещества, при котором происходит рассеяние света, сопровождающееся изменением частоты излучения [4,5].

Простое комбинационное рассеивание света можно рассматривать с двух точек зрения: классической и квантовой теории [6].

Рассмотрим простое комбинационное рассеивание света с точки зрения классической теории. Когда свет взаимодействует с молекулой вещества, то его электромагнитное поле обретает переменный дипольный момент молекулы. Изменения этого дипольного момента приводит к испусканию молекулой излучения во всех направлениях [1].

Запишем выражение интенсивности излучения света в скалярной форме:

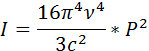
где ��−индуцированный дипольный момент, �� −скорость света, �� −частота излучения света

Так как электромагнитное поле светового излучения приобретает переменный дипольный момент молекулы, то его дипольный момент выражается формулой:

(1)

где ��−коэффициент пропорциональности, ��−напряженность поля.
В данном случае коэффициент пропорциональности �� можно назвать поляризованностью молекулы.

Рассмотрим излучение света как электромагнитное поле с напряженностью и циклической частотой :

(2)

где,−циклическая частота колебаний излучения, а−амплитуда колебаний

Подставив (2) в (1), получим:

(3)

Так как молекула имеет собственные колебания, то она будет иметь смещение ядер . Это смещение ядер будет иметь циклическую частоту колебаний молекулы, и его можно записать как:

(4)

где −циклическая частота колебаний молекулы, а−амплитуда колебаний.

При малых колебаниях молекулы коэффициент пропорциональности будет линейно зависеть от смещения ядер и будет ограничиваться дифференциальным уравнением первого порядка:

(5)

где −полризованность молекулы в точке равновесия,
−производная поляризованности молекулы по смещению ядер в точке равновесия.

Подставив (4) в (5), получим:

(6)

Подставив (6) в (3), получим:

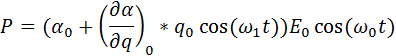
Раскроем скобки:

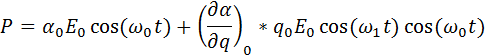
Воспользуемся формулой из тригонометрии:

(3)

Получим:

Учитывая, что: , получим:

Подставив выражение дипольного момента в выражение интенсивности излучения света, можно сделать вывод:

При облучении молекулы монохроматической волной света, молекула рассеивает излучение не только с частотой , но и с частотами .

Рассмотрим простое комбинационное рассеивание с точки зрения квантовой теории.

Фотон имеет энергию:

где ℎ−постоянная Планка,−частота излучения

При столкновении фотонов с молекулой вещества, фотоны рассеиваются. Так как столкновение является неупругим, то между каждым фотоном и молекулой произойдет обмен энергией. Получается, что энергия фотона изменится на какое-то количество энергии:

Зная, что , получим:

Где мы так же получаем изменение частоты излучения.

Причем:

-это стоксовое излучение.

-это антистоксовое излучение.

Проанализируем вынужденное комбинационное рассеивание света.

Если увеличивать интенсивность света, то в результате простого комбинационного рассеивания света интенсивность стоксового излучения будет увеличиваться. В таких условиях молекула взаимодействует с двумя электромагнитными излучениями:

1. с излучением, имеющим частоту:

2. с излучением, имеющим частоту: (стоксовое излучение)
где - частота излучения световой волны, - собственная частота колебаний молекулы.

Тогда энергия взаимодействия между светом и молекулой будет иметь вид:

где ��−дипольный момент, ��−напряженность поля.

Известно, что . Преобразуем предыдущее уравнение:

В этом случае возникает сила:

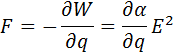
Эта сила будет действовать на собственные колебания молекулы только в том случае, когда . Если это условие выполняется, то при наличии в электромагнитном поле компонентов, разность которых приближена к собственным колебаниям молекулы, происходит неустойчивость монохроматической волны. Если впоследствии неустойчивости интенсивность стоксового излучения превышает пороговое значение, то она начинает увеличиваться экспоненциально.

где - начальное стоксовое излучение, - коэффициент усиления, - интенсивность световой волны, ��−длина возбужденной части среды.
Коэффициент усиления зависит от многих факторов, но в основном от плотности молекул и сечения рассеивания.

Научный руководитель: к.п.н., доцент С.А.Мищик

ЛИТЕРАТУРА:

1. Бенуэлл К. Основы молекулярной спектроскопии: Пер. с анг. М.: Мир, 1985. — 384 с.

2. В. Л. Гинзбург В. Л. , Фабелинский И. Л.  К истории открытия комбинационного рассеяния света// Вестник Российской Академии Наук. – М.: Том 73, № 3, с. 215-227 (2003) .

3. Кольрауш К. Спектры комбинационного рассеяния. Перевод с немецкого Батуева М.И., Маянца Л.С. Под редакцией и со вступительной статьей Ландсберга Г.С. - М.: Изд-во Иностранной литературы. 1952г. 466 с.

4. Ландсберг Г. С., Мандельштам Л. И. Новое явление при рассеянии света. Журнал Русского физико-химического общества. – М.: 1928. Т. 60. - С. 335.

5. Фабелинский И. Л. К 50-летию открытия комбинационного рассеяния света, 1978.- М.: Т. 126, вып.1. Стр. 123—152.

6. Фабелинский И. Л. Комбинационному рассеянию света —70 лет.
1998.- М.: Т. 168, № 12. Стр. 1342—1360.