Технические науки/5. Энергетика
К.т.н. В.С.
Павлюков, С.В. Павлюков
Южно-Уральский государственный
университет (НИУ), Россия
Модель для анализа
электрических систем в пространстве
комплексно-сопряженных
режимных параметров
Введение
Анализ и управление электроэнергетическими
системами, как очень больших и сложных электротехнических комплексов, должны
базироваться на современных математических моделях. Поиск и разработка новых
моделей всегда актуальны, тем более в условиях появления новых
электротехнических технологий, которые способствуют развитию направления интеллектуального управления
режимами электрических систем.
Данная математическая модель представляет
подзадачу комплексной задачи, связанной с поиском эксплуатационной схемы
распределительной сети оптимальной по потерям электроэнергии с учетом питающей
высоковольтной сети.
Модель должна решать несколько вопросов,
главные из которых: определения эффективным способом разностей напряжений между
узлами связи питающей и распределительной сетями, частных производных функции
потерь электроэнергии высоковольтной сети для суммарного градиента обеих сетей.
Наиболее полный учет питающей сети в
комплексной задаче, очевидно, может выполняться на основе расчета
установившегося режима питающей сети. На каждом итерационного шаге решения
задачи оптимизации эксплуатационной
схемы распределительной сети необходимо
вычислять градиент целевой функции. В связи с большой размерностью обозначенной
задачи к расчетам установившихся режимов, с помощью которых требуется
определять ряд параметров, играющих важную роль при формировании целевой
функции, должны быть предъявлены требования компактности, быстродействия и
простоты при алгоритмизации для комплексной задачи. Все перечисленные параметры
могут быть получены по результатам расчета установившегося режима питающей сети
с использованием новой технологии. Следует заметить, что этот подход может
рассматриваться не только как вспомогательная подзадача, но иметь и самостоятельное
значение.
Теоретическая часть
Подзадача расчета установившегося режима
математически формулируется как решение системы нелинейных уравнений,
связывающих мощности и токи или напряжения(режимные параметры) в элементах
питающей сети. Связь между режимными параметрами сети может быть записана для
векторных узловых или контурных переменных. Уравнения в контурной форме для
питающей сети имеют тот недостаток, что при помощи них нельзя непосредственно
связать мощности узлов с соответствующими величинами узловых напряжений, а с
ростом коэффициента связности усложняется выбор независимых контуров [1]. Поэтому рассмотрение указанной подзадачи
будет базироваться на использовании уравнений в ![]() – форме, которые
записываются в виде [2]
– форме, которые
записываются в виде [2]
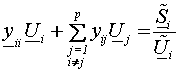 (1)
(1)
или
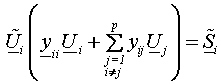 , (2)
, (2)
где ![]() – напряжение в
узлах сети
– напряжение в
узлах сети![]() ;
; ![]() – мощность в узлах сети;
– мощность в узлах сети; ![]() – узловые параметры схемы замещения сети;
– узловые параметры схемы замещения сети; ![]() – число узлов в схеме сети, не считая балансирующего.
– число узлов в схеме сети, не считая балансирующего.
Вид
уравнений установившегося режима (1) или (2) будет зависеть от
конкретной схемы замещения питающей сети [2].
Линейная часть сети замещена пассивным многополюсником, к полюсам
которого ![]() присоединяются
нелинейные элементы (генераторы, нагрузки). Замещение схемы питающей сети
матрицей
присоединяются
нелинейные элементы (генераторы, нагрузки). Замещение схемы питающей сети
матрицей ![]() позволит при алгоритмизации подзадачи расчета
установившегося режима использовать ее важные свойства: симметричности, наличие
большого числа нулевых элементов. При учете указанных свойств матрицы
позволит при алгоритмизации подзадачи расчета
установившегося режима использовать ее важные свойства: симметричности, наличие
большого числа нулевых элементов. При учете указанных свойств матрицы ![]() достигается
компактность и ускорение расчетов установившегося режима, что уменьшает время
итераций основной задачи оптимизации. Уравнения установившегося режима для
схемы замещения могут составляться относительно полных напряжений, включая
напряжение балансирующего узла. При отсутствии заземленной точки уравнения
установившегося режима моделируются для превышения напряжений узлов
достигается
компактность и ускорение расчетов установившегося режима, что уменьшает время
итераций основной задачи оптимизации. Уравнения установившегося режима для
схемы замещения могут составляться относительно полных напряжений, включая
напряжение балансирующего узла. При отсутствии заземленной точки уравнения
установившегося режима моделируются для превышения напряжений узлов ![]() относительно
уровня напряжения балансирующего узла. Полное напряжение
относительно
уровня напряжения балансирующего узла. Полное напряжение ![]() –го узла будет определяться по формуле
–го узла будет определяться по формуле
![]() ,
,
где ![]() – напряжение балансирующего узла;
– напряжение балансирующего узла; ![]() – превышение напряжения
– превышение напряжения
![]() – го узла;
– го узла; ![]() – индексы, соответственно, обозначающие действительную
и мнимую части комплексного числа.
– индексы, соответственно, обозначающие действительную
и мнимую части комплексного числа.
Расчет установившегося режима питающей
сети проводится по следующим исходным данным:
1) напряжению в балансирующем узле;
2) топологии схемы замещения питающей сети и схемных
параметров ее ветвей;
3) активной и реактивной мощностям в узлах или других
режимных данных;
4) заданной точности по напряжениям и
небалансу мощностей в узлах.
Тип задания исходных данных может
изменяться. Следует заметить, что конфигурация сети задается традиционным
способом: для каждой ветви указываются номера концевых узлов и полные сопротивления, которые могут
храниться в базе данных информационно-вычислительных комплексов.
Нагрузка в узлах присоединения питающей к распределительной сети
определяется текущим положением оптимизируемых размыканий контуров и находится
суммированием токовых нагрузок, присоединенных к узлу фидеров распределительной
сети. Полученные в результате расчета узловые напряжения используются для
определения других параметров режима, например, разности напряжения ![]() между узлами присоединения распределительной сети
к питающей, потерь электроэнергии в
исходном режиме и, наконец, составляющих градиента целевой функции, упомянутой
выше.
между узлами присоединения распределительной сети
к питающей, потерь электроэнергии в
исходном режиме и, наконец, составляющих градиента целевой функции, упомянутой
выше.
Нелинейные уравнения узловых напряжений
(1) или (2) решаются итерационными методами, из которых наилучшим образом
удовлетворяет сформулированным требованиям метод расчета узловых напряжений,
представленный ниже.
Сущность рассматриваемого метода решения
нелинейной системы уравнений узловых напряжений состоит в следующем.
Предположим, что вектор напряжения ![]() есть результат
решения для
есть результат
решения для ![]() – го узла на
– го узла на ![]() итерационном шаге,
который отличается от точного решения для уравнений системы (2) на величину
итерационном шаге,
который отличается от точного решения для уравнений системы (2) на величину ![]() . Будем находить текущее
. Будем находить текущее ![]() приближение для
решения
приближение для
решения ![]() по формуле
по формуле
![]() , (3)
, (3)
где ![]() и
и ![]() есть число узлов
питающей сети, исключая балансирующий.
есть число узлов
питающей сети, исключая балансирующий.
Если учесть выражение (3) в системе уравнений (2) и пренебречь влиянием
членов ![]() , получим следующую систему уравнений в матричной форме
, получим следующую систему уравнений в матричной форме
![]() . (4)
. (4)
Последнее уравнение записано в матричной форме
относительно вектора неизвестных ![]() , заменивших
вектор
, заменивших
вектор ![]() переменных
переменных ![]() .
.
Векторы комплексных напряжений ![]() , мощностей
, мощностей ![]() , переменной
, переменной ![]() и матрицу узловых
проводимостей
и матрицу узловых
проводимостей ![]() разложим на
действительные и мнимые составляющие:
разложим на
действительные и мнимые составляющие:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
где ![]() и
и ![]() – соответственно элементы матриц активных и реактивных
узловых проводимостей схемы питающей
сети.
– соответственно элементы матриц активных и реактивных
узловых проводимостей схемы питающей
сети.
Указанные операции приводят к формированию
блочной матричной системы уравнений с
действительными коэффициентами
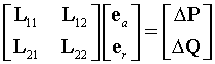 (5)
(5)
в пространстве переменных ![]() . Матрица коэффициентов
системы уравнений (5) состоит из четырех подблоков
. Матрица коэффициентов
системы уравнений (5) состоит из четырех подблоков ![]() ,
,![]() ,
,![]() ,
,![]() . Раскроем содержание матричных подблоков с использованием
ранее принятых обозначений схемных и режимных параметров.
. Раскроем содержание матричных подблоков с использованием
ранее принятых обозначений схемных и режимных параметров.
Элементы диагональных подблоков ![]() и
и ![]() вычисляются по
следующим формулам:
вычисляются по
следующим формулам:
 ;
; ![]() (6)
(6)
 ; (7)
; (7)
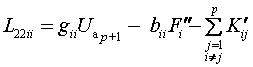 ; (8)
; (8)
![]() ,
(9)
,
(9)
где ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() – напряжение балансирующего узла
– напряжение балансирующего узла ![]() .
.
Расчетные формулы для элементов
недиагональных подблоков ![]() и
и ![]() моделируются
следующими выражениями:
моделируются
следующими выражениями:
 ; (10)
; (10)
 ; (11)
; (11)
 ; (12)
; (12)
![]() , (13)
, (13)
где ![]() .
.
Подблоки матрицы коэффициентов системы
уравнений (5) разрежены (имеют большое количество нулевых элементов) и
структурно подобны матрице узловых проводимостей ![]() . При этом использование методов работы с разреженными
матрицами [3] позволяет экономить память и сократить объем вычислений.
. При этом использование методов работы с разреженными
матрицами [3] позволяет экономить память и сократить объем вычислений.
Составляющие ![]() и
и ![]() правой части системы
(5), используя обозначения
правой части системы
(5), используя обозначения
![]() ,
, ![]() ,
, ![]() ,
,
выразятся
как
 ;
(14)
;
(14)
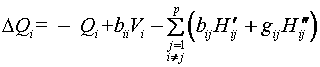 .
(15)
.
(15)
Вектор искомых переменных определяется с
помощью итерационного решения матричной системы уравнений (5). При этом
приближения предполагаются вычисленными
на предыдущем итерационном шаге. Итеративный процесс решения системы уравнений
(5) начинается с принятого вектора начального приближения ![]() . Для итерационного процесса формируется матрица
коэффициентов по формулам (6) – (13) и корректируется правая часть по
выражениям (14) – (15) для указанной системы уравнений. Вектор новых приближений
вычисляется решением полученной линеаризованной системы в окрестности текущих
приближений внутри итерации с использованием прямых численных методов. Расчет
считается законченным, когда норма разности между значениями рассчитываемых составляющих
неизвестных в смежных итерациях меньше некоторой заданной величины
. Для итерационного процесса формируется матрица
коэффициентов по формулам (6) – (13) и корректируется правая часть по
выражениям (14) – (15) для указанной системы уравнений. Вектор новых приближений
вычисляется решением полученной линеаризованной системы в окрестности текущих
приближений внутри итерации с использованием прямых численных методов. Расчет
считается законченным, когда норма разности между значениями рассчитываемых составляющих
неизвестных в смежных итерациях меньше некоторой заданной величины ![]() для всех неизвестных
одновременно:
для всех неизвестных
одновременно:
![]() ;
;
![]() .
.
После
заключительной итерации определяются вышеуказанные параметры и в том числе вектор разности
напряжений ![]() , которые входят в выражение градиента потерь целевой
функции. Эти напряжения вычисляются, как указывалось ранее, только между теми
узлами связи сетей, которые входят в цепи контуров распределительной сети, замыкающихся
через питающую сеть.
, которые входят в выражение градиента потерь целевой
функции. Эти напряжения вычисляются, как указывалось ранее, только между теми
узлами связи сетей, которые входят в цепи контуров распределительной сети, замыкающихся
через питающую сеть.
Вычислительный эксперимент
Эффективность данного метода
сопоставлялась с методом Ньютона [1] , принятого в качестве эталонного. Скорость
сходимости двух методов оценивалась по нормам разности диагональных и не диагональных элементов, соответственно матриц коэффициентов Якоби ![]() и уравнений (5) установившегося режима [1,2]. Чем меньше
разность, тем ближе к эталонному скорость сходимости итерационного процесса,
описываемого указанными уравнениями. В
данном случае нормы разности диагональных
и уравнений (5) установившегося режима [1,2]. Чем меньше
разность, тем ближе к эталонному скорость сходимости итерационного процесса,
описываемого указанными уравнениями. В
данном случае нормы разности диагональных
![]() и недиагональных
элементов
и недиагональных
элементов ![]() вблизи решения
установившегося режима питающих сетей 150 и 300 узлов были малы по сравнению соответственно с нормами диагональных
вблизи решения
установившегося режима питающих сетей 150 и 300 узлов были малы по сравнению соответственно с нормами диагональных ![]() и недиагональных
и недиагональных ![]() коэффициентов матрицы
Якоби. Если норма разности стремится к нулю, то согласно [4], сходимость
рассматриваемого метода расчета вектора комплексных напряжений в узлах аналогична
скорости сходимости эталонного метода.
коэффициентов матрицы
Якоби. Если норма разности стремится к нулю, то согласно [4], сходимость
рассматриваемого метода расчета вектора комплексных напряжений в узлах аналогична
скорости сходимости эталонного метода.
Выводы
В рамках задачи оптимизации
эксплуатационных схем распределительной сети, предложенная модель представляет
отличную технологию от существующих, определения узловых и других режимных
параметров, в том числе определение
разности напряжений между узлами связи сетей, которые, стоит заметить, входят только в цепи контуров распределительной
сети, замыкающихся через питающую сеть и позволяющая избежать применения
трудоемких операций, связанных с формированием матриц частных производных на
базе узловых уравнений в форме баланса мощностей[2].
Литература:
1.
Идельчик В.И.
Электрические системы и сети. – М.: Энергоатомиздат,1989. – 592с.
2.
Электрические системы.
Электрические сети / под ред. В.А. Веникова, В.А. Строева. – М.: Высшая школа,
1998. – 512 с.
3.
Тьюарсон Р. Разреженные
матрицы. – М.: Мир, 1977. – 190 с.
4.
Воеводин В.В., Кузнецов
Ю.А. Матрицы и вычисления. – М.: Наука, 1984. – 320 с.
5.
Боглаев Ю.П.
Вычислительная математика и программирование: Учеб. пособие. – М. : Высшая
школа, 1990. – 544 с.