КОМПЬЮТЕРЛІК ТОМОГРАФИЯНЫҢ НЕГІЗГІ ТЕҢДЕУЛЕРІ

Рентгендік компьютерлік томографияда ақпарат ретінде рентгендік фотондар, яғни функциясымен сипатталатын сәулелендіру ағыны қолданылады, мұндағы – кеңістік координаталары, – бұрыштық координаталар, ал Е – фотондар энергиясы. Рентгендік фотондар тығыздығын сипаттайтын функцияны деп белгілейміз. Сонда сызықтық әлсіреу коэффициентті болатын заттағы рентгендік фотондардың таралуы келесі

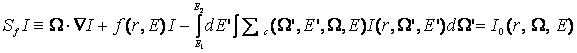
теңдеуімен анықталады [19], мұндағы – релейлік және комптондық таралудың макроқимасы. Көпшілік жағдайда операторын айқын түрде анықтау қиындық туғызады. Сондықтан операторының айқын түрін анықтаудың қарапайым мүмкіндігін қарастыру керек.

Айталық сәулелендіру ағынының функциясын келесі Нейман

(1)

қатары түрінде жазайық, мұндағы – бастапқы рентгендік фотондар ағыны, – п еселі рентгендік фотондардың ағыны . Рентгендік томографтың сканерлеу схемасын анықтау -ке байланысты.

операторын

(2)

түрінде алуға болады, мұндағы – қайнар көзінің қуаты, – Дирактың дельта функциясы, – қайнар көзінің координатасы, – қайнар көзінің коллимациясының бағыты, – рентген фотондарының энергиясы.

Соңғы (2) формуласынан операторына кері операторын табу есебі оңай екендігін байқаймыз. Шынында да, (2) теңдеуін өрнегіне байланысты шеше отырып және айнымалысын алмастыра отырып ( – жазықтықтағы түзудің координаталары),

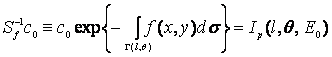(3)

теңдеуін аламыз, мұндағы – сәулелендіру қайнар көзінің ағыны, ал – сәулелендіру таралатын сызық.

Мұндай сканерлеу схемасына қайнар көз – детектор жұбының айналу қозғалысы тән (сондықтан үшінде). Осыны тұжырымдау үшін бас нүктенің маңайында айналуға инвариантты болатын сызықтар жиынын қарастырайық.

Айталық U операторы функциясын функциясына көшіретін

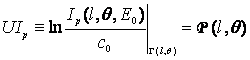(4)

түріндегі операторы болсын. Сонда (3) және (4) формулаларынан компьютерлік томографияның

(5)

түріндегі негізгі теңдеуін аламыз.

Айталық сәулелендіру ағынының функциясы (1) түрінде анықталсын. Сонда п еселі рентген фотондары үшін

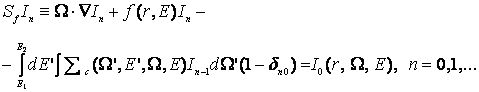(6)

теңдеуін аламыз, мұндағы – Кронекер символы [19]. Бұл теңдеудің шешімін

(7)

түрінде жазуға болады, мұндағы

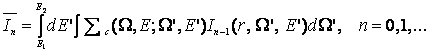
(6) және (7) формулаларын қолдана отырып, тасымалдау теңдеуін шешу есебін көп еселі интегралдар тізбегін есептеуге келтіруге болады. Сонымен бұл жағдайда операторы айқындалмаған түрде беріледі. Компьютерлік томографияның негізгі теңдеуі

(8)

түрінде анықталады, мұндағы U операторы функциясын функциясына көшіретін оператор.

(8) теңдеуінің функциясынан сызықты емес екендігін байқаймыз. Бұл жағдайда операторы ретінде

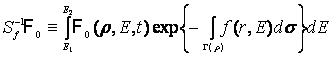(9)

өрнегін алуға болады. Мұндағы белгілі оң функция; – компоненттері зерттелетін объектінің қасиеттерін сипаттайтын сандық параметр болатын вектор; – рентгендік сәулеленудің әлсіреуінің сызықтық коэффициентінің таралуы.

Егер функциясын

(10)

түрінде жазатын болсақ, мұндағы – кесіндісінде монотонды кемімелі және функциясына қарағанда өте аз болатын аналитикалық функция, онда операторын аппроксимациялайтын операторын құруға болады және оны

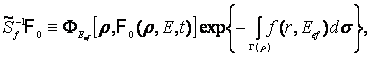
(11)

түрінде жазуға болады.