Технические науки.Энергетика

Магистрант Тулегенов Е.Е., профессор Айталиев Е.С.

Западно-Казахстанский аграрно-технический университет имени Жангир хана, Казахстан

Теоретический анализ ветроэнергетических установок

В данном статье приводится методика определения мощности, крутящего момента и силы сопротивления, действующих на ветроколесо. В этом анализе будем использовать линейное приближение.

В отсутствие турбулентности объем воздуха, проходящего в единицу времени через поперечное сечение ветроколеса площадью А(рисунок 1), обладает кинетической энергией, равной:

P₀=0,5(ρA₁ U₀)U₀²=0,5ρA₁U₀³ .(1)

где ρ и U₀– плотность и скорость набегающего воздушного потока. Таким образом, Р₀ есть кинетическая энергия ветрового потока.

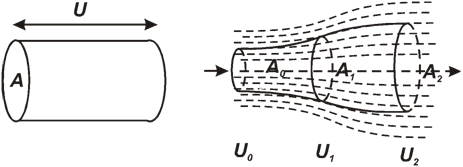
Рисунок 1. Схема к расчету мощности ветрового потока и модель взаимодействия ветрового потока с ветроколесом

Плотность воздуха r зависит от высоты над поверхностью Земли, а также метеорологических условий. Скорость ветра увеличивается с высотой, зависит от местных географических условий и довольно сильно меняется во времени. Для расчета будем считать, что скорость ветра U₀ и плотность ρ являются постоянными во времени и в любом поперечном сечении воздушного потока. На уровне моря плотность воздуха равна 1,2 кг/м³, а необходимая для эффективной работы ветроустановки скорость ветра – порядка 10 м/с. При этих данных энергия ветра Р₀ =600 Вт/м². При штормовом ветре U₀ ~ 25 м/c, тогда Р_o ~ 10000 Вт/м².

В теории ветроколеса предполагается, что проходящие через него линии тока не претерпевают разрыва, а само колесо заменяется таким проницаемым диском, при взаимодействии с которым воздушный поток отдает ему часть энергии, в силу чего давление в потоке и его импульс уменьшаются. Кроме того, в процессе взаимодействия в набегающий ламинарный поток вносятся различные возмущения, но здесь и в дальнейшем мы ими можем пренебречь.

На рисунок 1, величина А₁– площадь, ометаемая ветроколесом, А₀ и А₂– площади поперечных сечений проходящего через ветроколесо потока соответственно до и за ним, причем сечение А₀ расположено за пределами возмущенной ветроколесом области, а сечение А₂– в месте наименьшей скорости потока. Положение площадей А₀ и А₂ можно определить по результатам экспериментальных измерений поля скоростей в окрестности ветроколеса. Непосредственно в сеченииА₁ провести такие измерения нельзя из-за вращения ветроколеса.

Действующая на ветроколесо сила F₁, равна изменению количества движения массы проходящего через него в единицу времени воздуха ṁ, то есть можно считать, что

F=U₀–U₂ .(2)

Эта сила действует на ветроколесо со стороны протекающего через него воздушного потока, который можно считать однородным и имеющим скорость U₁. Мощность, развиваемая этой силой, будет иметь вид:

Р = FU₁ = (U₀–U₂)U₁ .(3)

Но эта мощность Р есть энергия, теряемая в единицу времени ветровым потоком, взаимодействующим с вветроколесом, которая равна:

P_w= 1/2 (U₀²–U₂²) . (4)

Приравнивая (3) и (4), получим:

(U₀–U₂)U₁= 0,5 (U₀²–U₂²) = 0,5(U₀–U₂) (U₀+U₂) . (5)

Масса воздуха, проходящего через поверхность А₁, ометаемой ветроколесом в единицу времени,

F= r А₁ U₁ . (6)

Тогда (3) примет вид:

P = r А₁ U₁² (U₀ – U₂) . (7)

А после замены U₂ из (6) получим

P = r А₁ U₁² (U₀ – (2U₁ – U₀)) = 2 ρ А₁ U₁²(U₀ – U₁). (8)

Обозначим через а величину:

а = (U₀– U₁)/ U₀ , (9)

называемую коэффициентом торможения потока.

Тогда величина скорости будет иметь вид:

U₁ =(1 –a ) /U₀ .(10)

Но с учетом (5) и (9)

а = (U₀–U₂)/(2U₀) . (11)

Очень часто величину а также называют коэффициентом индукции или возмущения.

Подставляя U₁ из (10) в (8), получим:

P = 2rА₁(1-а)² U₀² [U₀ – (1 –a) U₀] = 0,5r A₁U₀³[4a(1-a)²] . (12)

Сопоставляя это выражение с (1), получим для мощности

Р = С_рР₀, (13)

где, Р₀– мощность набегающего потока; С_р– часть этой мощности, передаваемая ветроколесу (эту часть называют коэффициентом мощности), равная:

С_р= 4 а (1 – а²) . (14)

Иногда вместо коэффициента а применяют коэффициент b = U₂/U₀, также называемый коэффициентом торможения потока.

Легко показать, что максимальное значение коэффициента С_р имеет величину:

С_{р max}= 16/27 = 0,59 . (15)

Таким образом, в лучшем случае только немногим более половины энергии набегающего ветрового потока можно использовать для преобразования кинетической энергии потока в энергию вращения ветроколеса. Это объясняется тем, что воздушный поток должен обладать определенной кинетической энергией, чтобы покинуть область ветроколеса. Равенство (15) называется критерием Бетца.

Лобовое давление на ветроколесо

Течение идеального газа (или жидкости) описывается уравнением Бернулли. Воспользуемся этим уравнением для определения нагрузки, испытываемой ветроколесом с горизонтально-осевым расположением генератора. Эта нагрузка возникает вследствие разности давлений Dр в набегающем потоке непосредственно до и после ветроколеса (рисунок 3), которое, как и раньше, будем считать проницаемым диском площадью А₁.

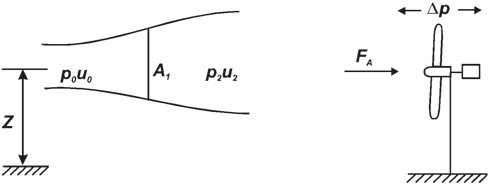
Рисунок 2. Лобовое давление на ветроколесо: U – скорость ветрового потока; Р – давление; Z – высота; F_A – осевая нагрузка; Dр – разность давлений

Максимальный перепад давления будет в случае, если U₂ =0. Таким образом,

Dр_max = 0,5 r U₀² , (16)

а максимальная нагрузка, действующая на ветроколесо, будет

F_Amax= 0,5ρA₁U₀². (17)

В горизонтально-осевых ВЭУ эта сила действует по оси ветроколеса и называется лобовым давлением.

Очевидно, действуя на ветроколесо, сила равна скорости изменения количества движения набегающего воздушного потока:

F_A= (U₀–U₁) . (18)

Используя (6), (9) и (11), получим

F_A=(ρA₁U₁)(2U₀ a)= ρ A₁(1 – a)U₀(2U₀a) =0,5ρA₁U₀² × 4a (1-a). (19)

В приближении предлагаемой модели член 0,5ρ*A₁*U₀² равен силе, действующей на находящийся в потоке непроницаемый диск площадью А₁.

С_F–коэффициент лобового давления, зависящий от параметров ветроколеса, имеет вид:

С_F= 4*а*(1 – а) . (20)

При а= 0,5 величина С_F=1, что соответствует значению U₂ = 0. Согласно критерию Бетца, максимальный КПД ветроколеса достигается при а= 0,33, и ему соответствует значение С_F= 8/9.

Из-за краевых эффектов коэффициент лобового сопротивления непроницаемого диска на самом деле превышает единицу и равен примерно 1,2. Тем не менее, применяющаяся здесь линейная теория показывает, что представление ветроколеса почти непроницаемым диском в теоретических расчетах вполне оправдано. Представление об обтекании ветроколеса, как о течении невозмущенного потока воздуха в промежутках между лопастями, является неточным.

Особенно неприемлемо такое представление при работе ветроколеса с высоким КПД, когда оно оказывает максимальное сопротивление ветровому потоку.

Величина 0,5ρA₁U₀² и соответствующая ветровая нагрузка быстро возрастают с увеличением скорости ветра и, как правило, ветроколёса не выдерживают нагрузок со скоростью выше ~20 м/с. Для предупреждения их разрушения в этом случае используют следующие способы:

а) поворот ветроколеса или его лопастей в нерабочее положение;

б) уменьшение снимаемой мощности и соответственно лобового давления;

в) применение лопастей такого профиля, чтобы они способствовали самоторможению при такой скорости ветра;

г) принудительную остановку ветроколеса.

Использование в ветроколесе неподвижных самотормозящихся лопастей – это наиболее простой и дешевый способ, обеспечивающий безаварийную работу ВЭУ, однако при этом не всегда удается достичь высоких значений КПД при нормальных ветровых условиях.

Крутящий момент

Для определения крутящего момента (момента силы) на выходе ветроколеса можно воспользоваться результатами расчетов лобового давления. При таком подходе не используется закон сохранения момента импульса в системе ветроколесо – набегающий поток, который здесь использовать довольно затруднительно.

Максимальный крутящий момент ветроколеса Т_max очевидно, не может превышать значения, равного произведению максимальной действующей на ветроколесо силы на максимальный радиус R, т.е.

T_max=F_maxR, (21)

так как величина максимальной силы определяется сопротивлением, т.е.

F_max=ρA₁ U/ 2 . (22)

Следовательно,

T_max= 0,5ρA₁ UR. (23)

В общем случае крутящий момент ветроколеса Т можно представить в виде

Т = С_тТ_max, (24)

где С_т–коэффициент крутящего момента.

Введем в рассмотрение параметр Z, называемый быстроходностью ветроколеса, равный отношению окружной скорости конца лопастей V_r к невозмущенной скорости набегающего потока U₀,т.е.

Z = V_r/U₀ = R w / U₀ , (30)

где w – угловая скорость вращения ветроколеса.

Тогда, заменяя в (22) значение Rего выражением из (25), получаем:

T_max = r A₁ U₀² (U₀Z)/2w = P₀Z/w , (26)

где Р₀– мощность ветрового потока из (2).

Так как мощность на валу есть мощность, развиваемая ветроколесом Р, то

Р = Т_max w . (27)

Но согласно (13) Р = С_р*Р₀, или, с учетом уравнений (24) и (26) равенство (27) примет вид:

С_р Р₀ = С Т_max w; С_р Р₀ = С_т Р₀ Z; C_р = Z C_т . (28)

Отметим, что на практике коэффициенты C_р иC_т не постоянны, являются функциями Z.

Согласно критерию Бетца (15), максимальное значение коэффициента С_р равно 0,59, поэтому в идеальном случае имеем:

(С_т)_max= 0,59/Z. (29)

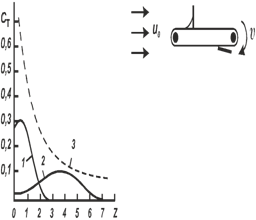
Рисунок 3. Характеристики реальных ветроколес. Зависимость коэффициента крутящего момента С_т от быстроходности Z для ветроколес с высоким геометрическим заполнением (1), низким (2) и критерий Бетца (3)

Из рисунка 3 видно, что ветроколеса с высоким геометрическим заполнением развивают большой крутящий момент при относительно низких линейных скоростях, и, наоборот, ветроколеса с небольшим заполнением (например, с двумя лопастями) имеют небольшой крутящий момент, и даже иногда не могут самостоятельно раскрутиться. С увеличением значений Z коэффициент момента, а следовательно, и сам момент стремится к нулю. Максимальные значения коэффициента С_т для одних типов ветроколес реализуются при высоких скоростях ветра, при которых лобовые давления велики – вплоть до разрушительных. Необходимо также отметить, что максимальным значениям крутящего момента и КПД соответствуют различные значения Z.

Литературы

1. Фалеев Д.С. «Возобновляемые и ресурсосберегающие источники энергии.» издание 4-е. Рекомендовано МТС РФ в качестве учебного пособия для вузов ж.д. транспорта. Хабаровск 2005.

2. Фалеев Д.С. Фалеев Д.С. «Возобновляемые и ресурсосберегающие источники энергии.» издание 3-е. ДВГУПС. Хабаровск 2004.

3. Ветроэнергетика/ Под ред. Д. де Рензо: Пер. с англ.; В 39 под ред. Я.И.Шефтера.- М.: Энергоатам издат, 1982.