Bulhakov M.O.

SHEI “National Mining University”, Ukraine

Mathematical model of DDoS-attack

A distributed denial-of-service (DDoS) attack is a malicious attempt to disrupt normal traffic of a targeted server, service or network by overwhelming the target or its surrounding infrastructure with a flood of Internet traffic. DDoS-attacks achieve effectiveness by utilizing multiple compromised computer systems as sources of attack traffic. Exploited machines can include computers and other networked resources such as IoT devices.

A DDoS-attack requires an attacker to gain control of a network of online machines in order to carry out an attack. Computers and other machines (such as IoT devices) are infected with malware, turning each one into a bot (or zombie). The attacker then has remote control over the group of bots, which is called a botnet.

Once a botnet has been established, the attacker is able to direct the machines by sending updated instructions to each bot via a method of remote control. When the IP address of a victim is targeted by the botnet, each bot will respond by sending requests to the target, potentially causing the targeted server or network to overflow capacity, resulting in a denial-of-service to normal traffic. Because each bot is a legitimate Internet device, separating the attack traffic from normal traffic can be difficult.

Let us suppose that the attacked node has an inbound channel with a bandwidth of C bit/s, and an edge router has an input buffer of B bits. The attack situation can be simulated using a model of statistical multiplexing of traffic from N attacking nodes, which can be in two states: sending packets (ON-state) and inactivity (OFF-state).

We denote the time periods (in seconds) of functioning and inactivity as and respectively. If the source is active (ON-state), then it generates r packets per second. The size of the sent packet in bits will be denoted by L, and the volume of received packets at time t as Q (t).

Then the buffer overload probability can be approximated by the formula:

where

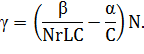
To cause an overload on the transmission channel, the attacker must select attack parameters such that the value of γ is close to zero or negative. Therefore, the number of nodes for the attack must satisfy the inequality

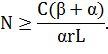
Let us call the ratio of the duration of sending packets to the whole period of operation and inactivity as the coefficient of employment of the traffic source τ:

Then the inequality limiting the number of attacking nodes can be expressed as

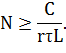
In typical ICMP-flood attacks, the attacking nodes are constantly in the ON-state, sending parasitic traffic to the victim. In this case, the coefficient τ = 1 and the inequality for the number of attacking nodes is simplified to

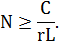
To make it difficult to recognize the attack the attacker masks it under the usual overload in the network. To do this he needs to choose rather small values for the parameters τ and r.

So if an attacker chooses values of τ = 0,05 and r = 20 pack/s and the attack target is a server with a channel throughput of C = 10 Mbit/s, then 1,7 * 10⁴ attack nodes are required to attack.

In addition, an attacker can execute several processes on each of the attack nodes, and those using fictitious addresses of senders, can act for the attacker as various sources of traffic. Thus, it is quite realistic to implement a distributed DoS-attack masking it under the natural overload of the channel.

The conclusions drawn can be generalized to different types of attack sources. Let the attacker have M different types of attacking nodes. Then the attacker must choose the attack parameters so that the following relation is true:

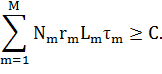
An attacker can generate traffic that does not cause suspicion and is similar to traffic from a normal user, having at his disposal a sufficient number of N controlled nodes. Basing on some collected statistics on network state dynamics (for example, packet loss level) it is possible to estimate the future states of the system under study.