Современные информационные технологии/ 2. Вычислительная техника и программирование

Постол А.С.

Национальный горный университет, Украина

Информационная технология нейровейвлетной идентификации и моделирования объектов в задачах АСУ

Метод саморегулирования является важным соображением для проектирования системы для построения адаптивных контроллеров неизвестной медленно меняющейся системы. Основная идея в адаптивном управлении состоит в том, чтобы оценить неопределенные параметры установки и соответственно отрегулировать параметры управления он-лайн, на основе измеренных сигналов системы, используя оценочные параметры под контролем входных вычислений.Зачастую нет возможности представить адекватные характеристики системы, такие как нелинейность, временная задержка, насыщенность, изменяющиеся во времени параметры в общей сложности. Важно разработать эффективную технику в которой структура нелинейной модели может быть идентифицирована с помощью адаптивного процесса.

Алгоритмы "wavenet" состоят из двух процессов: создание сетей и минимизация ошибок. В первом процессе, сетевые структуры, применяемые для представления, определяются с использованием вейвлета анализа. Сеть постепенно набирает скрытые блоки для эффективного и достаточного охвата частотной области. Одновременно сетевые параметры обновляются, чтобы сохранить топологию сети и воспользоваться преимуществами более поздних обработок. Во втором процессе минимизируются аппроксимации мгновенных ошибок используя метод адаптации, основанный на алгоритмах LMS. Параметр инициализированной сети обновляется с использованием метода градиента-спуска (сведения к минимуму). Каждый скрытый блок имеет квадратное окно в частотно-временной плоскости. Правило оптимизации применяется только к скрытым блокам, где выбранная точка попадает в их окна. Таким образом, длительность обучения может быть уменьшена.

Термин «вейвлет» означает небольшую волну. Эта маленькая волна должна иметь хотя бы минимальное колебание и быстрый спад до нуля как в положительном, так и в отрицательном направлениях его амплитуды. Это свойство аналогично условию допустимости функции, которая равна необходимости для вейвлет-преобразования [1]. На рис. 1.а, приведен пример вейвлета «Морлетный вейвлет», названный в честь изобретателя Жана Морле в 1984 году [2].

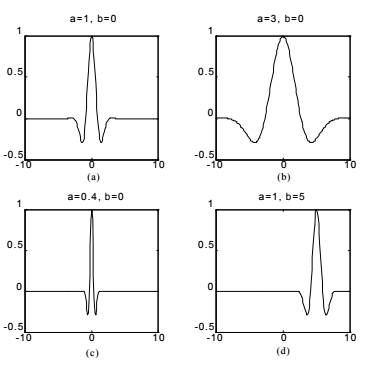
Рис.1. Вейвлеты Морле

Наборы «вейвлетов» используются для приближения сигнала, и цель состоит в том, чтобы найти набор дочерних вейвлетов, созданные расширенным (масштабированным или сжатым) и переведенным (сдвинутым) оригинальным вейвлетом, которые наилучшим образом представляют сигнал. Таким образом, «путешествуя» от больших масштабов к меньшим, один из них «масштабируется» и приближается все точнее к данному сигналу. На рис. 1b-d показаны различные дочерние вейвлеты, в которых а - является дилатацией, а b - трансляцией, соответствующей вейвлет-памяти Морле.

Выше показано саморегулирующееся управление эффективной архитектуры нейронной сети, основанной на теории вейвлетов, называемой "wavenets". Алгоритмы "wavenet" демонстрируют соответствующие топологии сети, изначально прибегая к методам проб и ошибок. "Wavenet" основанные на контроллерах, улучшают производительность обученной сети для быстрой конвергенции, минимальной изменчивости между прогонами, устойчивости к помехам и высокой сложной способности к изучению и отслеживанию неизвестных / неопределенных сложных систем.

Литература:

1. R. K. Young, "Wavelet Theory and Its Applications"; Kluwer Acadamic Publishers; Boston; 1993.

2. P. Goupillard, A. Grossmann, and J. Morlet Cycle-Octave and Related Transforms in Seismic Signal Analysis. -К.: Geoexploration, 1984. С. 85-102.