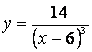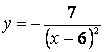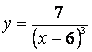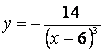ТестОВЫЙ КОНТРОЛЬ ЗНАНИЙ СТУДЕНТОВ
В РАМКАХ КОМПЕТЕНТНОСТНОГО ПОДХОДА
Стрельцова А.А, Гарькина И.А.
Пензенский
государственный университет архитектуры и строительства
Тестовый контроль
усвоения знаний студентов приобрел широкую популярность в связи с возможностями
наиболее объективной оценки знаний, более полного охвата программы,
значительного сокращения времени, затрачиваемого на проведение текущей и
промежуточной аттестации. Эти преимущества тестовых технологий по сравнению с
традиционными являются основополагающими. В рамках компетентностного подхода создаются фонды оценочных средств
(ФОС), обеспечивающие объективную оценку уровня сформированных компетенций в
условиях максимального приближения содержания, методов и средств контроля к
будущей профессиональной деятельности выпускников. При этом предполагается
проверять уровень остаточных знаний и умений в форме тестирования, а уровень сформированности владений
– в форме решения ситуативных заданий. В результате этого центральным местом ФОС являются тесты, составленные как для текущего,
так и промежуточного контроля. А в
условиях предельного ограничения количества аудиторных часов тестирование часто
является единственной возможностью формирования достаточно объективной оценки
знаний студентов.
Процесс изучения
математики бакалаврами, обучающимися по направлению 08.03.01 – Строительство, направлен
на формирование двух компетенций:
- ОПК-1: способность использовать основные законы
естественнонаучных дисциплин в профессиональной деятельности, применять методы
математического анализа и математического (компьютерного) моделирования, теоретического
и экспериментального исследования;
- ОПК-2: способность выявить естественнонаучную
сущность проблем, возникающих в ходе профессиональной деятельности, привлечь их
для решения соответствующий физико-математический аппарат.
В результате освоения
которых студент должен :
- знать фундаментальные основы высшей
математики, включая алгебру, геометрию, математический анализ, теорию
вероятностей и основы математической статистики;
- уметь самостоятельно использовать
математический аппарат, содержащийся в литературе по строительным наукам,
расширять свои математические познания;
- владеть первичными навыками и основными
методами решения математических задач из общеинженерных и специальных дисциплин специализации.
Приведем примерный
вариант тестов, направленных на реализацию ОПК-1 (знание основных математических формул и понятий; умение пользоваться математическим аппаратом
для решения задач; владение методами решения математических задач в профессиональной
деятельности), для проведения текущего контроля по теме «Производная».
1. Производная функции ![]() равна…
равна…
1).
![]() ; 2).
; 2).![]() ; 3).
; 3). ![]() ; 4).
; 4). ![]() .
.
2. Производная
функции y = xlnx в точке х = е равна…
1). 1; 2). 0; 3). 2; 4). –1.
3.Производная второго порядка функции ![]() равна…
равна…
|
1).
|
2).
|
3).
|
4).
|
4.Максимум функции ![]() равен …
равен …
|
1).
-3 |
2).
-2 |
3).
0 |
4).
36 |
5. Производная ![]() функции
функции 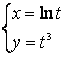 равна:
равна:
1).
![]() ; 2).
; 2). ![]() ; 3).
; 3). ![]() ; 4).
; 4). ![]() .
.
6.
Горизонтальная асимптота графика функции ![]() задается уравнением
вида…
задается уравнением
вида…
|
1).
|
2).
|
3).
|
4).
|
7. По плану периметр фундамента равен
1).
по ![]() м;
м; ![]() м;
м; ![]() м;
м; ![]() м; 3).
м; 3).
Обучение,
сопровождаемое тестированием (текущий и промежуточный контроль), является
эффективным инструментом для обеспечения качества подготовки бакалавров и
освоения ими определенных компетенций. Оно стимулирует студентов к
систематической самостоятельной работе с целью достижения высоких результатов,
а у преподавателя появляется дополнительная информация об уровне знаний
обучающихся, что дает ему возможность управлять познавательной деятельностью
каждого студента и повышать качество обучения.
Кафедрой
математики и математического моделирования Пензенского государственного
университета архитектуры и строительства в дополнении к ФОС разработаны и изданы
контрольно-измерительные и справочные материалы по всему курсу (КИМ) для
проведения тестов как по каждому модулю (текущая аттестация), так и по всему
курсу (промежуточная) дисциплины [1,2].
Разбор задач и примеров, приводимым в КИМах,
систематическое тестирование по ним в течение всего курса, позволяет бакалаврам
лучше подготовиться к промежуточной аттестации (зачет, экзамен).
Литература
1.Гарькина И.А., Данилов
А.М., Круглова А.Н. Математика. Часть I.
Справочные материалы и тесты по модулям. – Пенза: ПГУАС, 2013.- 328 с.
2. Гарькина
И.А., Данилов А.М., Круглова А.Н. Математика. Часть II. Тесты по общему курсу математики.
– Пенза: ПГУАС, 2013.- 208 с.