УДК 509.307.24
Абаполова
Е.А., Койда В.В., Примак И.М.
Белгородский
государственный национальный
исследовательский
университет
Моделирование эколого-экономического развития территориальных
образований
Анализ мировой хозяйственной практики в области регулирования
эколого-экономических отношений показывает, что одним из подходов, позволяющих
достичь согласования экологических и экономических интересов и потребностей
общества, является оценка потенциала развития социо-эколого-экономических
систем промышленных территорий на основе системы экологического управления.
Математическая модель эколого-экономического развития,
предлагаемая в работе, основывается на следующих предположениях:
- производственная функция задает соответствие между
вовлечением в процесс производства капитала, воспроизводимых и
невоспроизводимых природных ресурсов, с одной стороны, и выпуском некоторого «композитного»
продукта – с другой. Под «композитным» продуктом понимается произведенная в
процессе производства материальная субстанция, способная, благодаря своим
свойствам участвовать как в процессе непроизводственного потребления, так и в
процессе производства в качестве производственного капитала и, кроме того, – в
качестве воспроизводимого природного ресурса [1];
- имеет место взаимозаменяемость между результатом производства и
воспроизводимым природным ресурсом (опосредованная в реальной экономике
процессом очистки). Принимая концепцию композитного продукта, объединяем
функции производства и очистки, что упрощает дальнейший анализ;
- на рассматриваемом временном интервале
существует возможность агрегирования различных видов капитала,
невоспроизводимых и воспроизводимых природных ресурсов в скалярные величины Kt, Rt, Vt
соответственно;
- норма амортизации капитала – ka принята
постоянной;
- принимаются предположения относительно постоянства во времени величины
и структуры трудовых ресурсов
- известна величина запасов невоспроизводимых природных ресурсов и
состояние воспроизводимых в начальный момент времени. Возможность прямой
взаимозамены между ними полностью исключается;
- производственная функция является однородной первого порядка, вогнутой,
непрерывной и дифференцируемой на множестве своих аргументов;
- коэффициент приведения разновременных экономических показателей r не
меняется во времени.
При сделанных допущениях на уравнение, характеризующее функционирование
экономической системы налагается дополнительное условие о возвращении части «композитного»
продукта (в виде воспроизводимого экологического блага 
) в окружающую среду:
|
|
(1) |
Уравнение использования невоспроизводимых природных ресурсов
(2)
носит достаточно
простую форму и показывает изменение запасов невоспроизводимых природных
ресурсов Ś на величину их вовлечения в процесс производства R.
Экологическая сфера охватывает воспроизводимые, невоспроизводимые
природные ресурсы. Поскольку начальный объем невоспроизводимых ресурсов
известен и взаимосвязь «экономическая сфера – невоспроизводимые природные
ресурсы» определена, зададим динамику изменения воспроизводимых ресурсов. Для
этого воспользуемся уравнением Лотка-Вольтерра [2]
|
|
(3) |
описывающим процесс
естественного восстановления воспроизводимых природных ресурсов 
в зависимости от
естественного состояния окружающей среды 
, естественной нормы восстановления 
и текущего состояния
воспроизводимого природного капитала 
.
Включаем в это уравнение дополнительные переменные, учитывающие
взаимосвязь окружающей среды в части воспроизводимых природных ресурсов с
экономической системой.
|
|
(4) |
описывающее
зависимость изменения состояния воспроизводимых ресурсов от естественных
процессов восстановления и, кроме того, от их вовлечения в процесс производства
и регенерации за счет использования части произведенного композитного продукта.
Таким образом, в модели три фазовых переменных (K, S,
W). Начальное состояние задается
вектором (K0, S0, W0). Уравнения (1), (2), (4) в совокупности определяют
множество траекторий развития описываемой системы. На множество возможных
траекторий налагаются следующие условия: (K,
S, W) – непрерывные, (Ќ, Ś, Ẃ) – кусочно-непрерывные по времени функции.
Для нахождения эффективных стратегий эколого-экономического развития
зададим критерий, упорядочивающий их допустимое множество. Воспользуемся
утилитаристским критерием – критерием максимизации во времени приведенного
общественного благосостояния. Примем, что функция общественного благосостояния U = U(C, W) существует и
способна упорядочить между собой различные степени удовлетворения общественных
потребностей в зависимости от объемов потребления экономических благ и
состояния окружающей природной среды. Эта функция должна удовлетворять
следующим условиям:
- уровень благосостояния в какой-либо момент времени непосредственно не
зависит от благосостояния в любой другой момент времени;
- уровни благосостояния, соответствующие различным моментам времени,
сопоставляются с помощью постоянной положительной нормы дисконтирования, отражающей
общественную норму дисконтирования.
Таким образом, целевая функция может быть определена как
|
|
(5) |
.Задача оптимизации для агрегированной замкнутой
эколого-экономической системы с бесконечным горизонтом планирования и положительной
нормой дисконтирования заключается в выборе траекторий потребления, накопления
и использования воспроизводимых, невоспроизводимых природных ресурсов,
позволяющих максимизировать динамическую функцию общественного благосостояния.
Эта задача относится к классу задач оптимального
управления и решается с помощью принципа максимума Л.С.Понтрягина [4].
Литература:
1. Алексеев М. А. Методологические аспекты
эколого-экономического обоснования принятия хозяйственных решений.
Экономическое регулирование природопользования; Сб. науч. тр. Новосибирск; ИЭ и
ОПП СО РАН, 1992. С. 113-126.
2. Балацкой О.Ф. Экономический
потенциал административных и производственных систем. Сумы: ПТД «Университетская
книга», 2006. 973 с.
3. Лотка А. Дж. Элементы Физической Биологии.
Балтимор, 1925. (Переиздано под названием Элементы Математической Биологии.
Нью-Йорк: Дувр, 1956.). 321 с.
4. Интрилигатор М. Математические методы оптимизации и
экономическая теория. М.: Прогресс, 1975. 356 с.
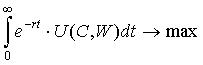