Докукова Н.А., Кафтайкина Е.Н., Кулаго А.Е.

Белорусский государственный университет

ДИНАМИКО-МАТЕМАТИЧЕСКАЯ ОПТИМИЗАЦИЯ МАШИНОСТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

Разработка виброизоляция машиностроительных конструкций состоит из множества инженерных, конструкторских и расчетных работ. После выбора подходящего макетного образца осуществляется его конструкторская проработка, составляется динамическая модель, за которой следует изучение математического аналога. Далее должны быть решены задачи, связанные с критериями выбора параметров, улучшающих качество такой модели. Это обстоятельство приводит к задачам математической оптимизации динамических свойств машиностроительной конструкции. Вследствие этого динамико-математическая оптимизация является оптимизацией динамической модели или систем уравнений движений, взаимодействующих между собой элементов, состоящая из нескольких этапов. На первом рассматривается математическая оптимизация колебательных режимов, возникающих во время эксплуатации мобильных машин в виброизолирующих элементах. На втором этапе находится динамический критерий для наиболее благоприятного режима движений, обеспечивающего быстрое затухание колебаний, или, наоборот, поддерживающего стабильные гармонические колебания с малыми амплитудами. На третьем определяются геометрико-физические зависимости в виде условий между параметрами. В результате получается нелинейная задача математического программирования [1].

Анализ представленного исследования предполагает реализацию нескольких основных критериев: затухание или гашение нежелательных колебательных режимов; изменение первой частоты собственных колебаний и ее перенос в область низких частот, стремление к нулю [2]; удовлетворение физических параметров динамической модели алгебраическим условиям устойчивости, например, В.С. Воронова для динамических процессов [3].

Постановка задачи. Задача движения подвески сидения транспортного средства [3] является нелинейной:

, (1)

(2)

Здесь x(t) - перемещение виброизолируемого тела, - его скорость, - ускорение, k - частота собственных колебаний, w_сопр - величина ускорения, полученная в результате деления силы сопротивления на общую массу, - нелинейные коэффициенты, g - ускорение свободного падения.

Величина ускорения силы сопротивления должна быть соизмеримой с максимальным нагрузочным режимом g(1-cos(wt)) за один цикл колебаний T=2p/w для минимизации общего баланса внешних сил. При этом динамика конструкции виброамортизатора обеспечивает перегрузку, не превышающую общий вес подвески сидения. Тогда минимальное значение функционала будет определять минимальное искомое значение ускорения d²x(t)/dt², которым должен обладать виброизолируемый объект. Вместе с этим, кинематические параметры не превышают оптимальных значений , , здесь b - коэффициент демпфирования амортизатора, c - коэффициент упругости пружины. К этим ограничениям следует добавить обезразмеренное физическое, описывающее энергетические потери в виде рассеивания тепла, отнесенные к единице массы, в результате преодоления сил гидродинамического сопротивления

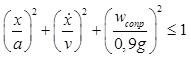. (3)

Введем множество переменных X=(x₁, x₂, x₃), где x₁ = x(t), x₂ = dx(t)/dt,
x₃= с ограничениями вида

, , , , (4)

на которых функционал

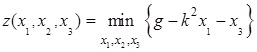(5)

принимает минимальное значение.

Применяя общую методику [1] к решению задачи (5), (4) из совокупности положительных координат x_j (j=), выбирается и фиксируется одна переменная. Пусть это будет х₃. Далее ищется максимум z по остальным переменным х₁, х₂. Полученное решение будет зависеть от выбранного х₃. Вследствие сепарабельности функционала z выделяется первая функция состояния с новыми условиями

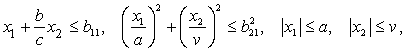, (6)

где , m - общая масса.

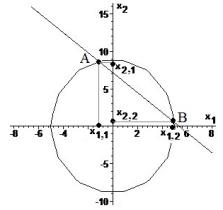
Величина Y_1,2 тем меньше, чем больше положительное значение x₁ . Для определения x₁ решим совместно систему неравенств (6) и выберем оптимальные параметры, геометрическая интерпретация которых представлена на рисунке 1

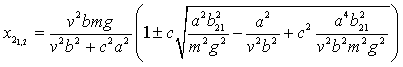, . (7)

Для того, чтобы приняло вещественные значения необходимо, чтобы подкоренное выражение в формуле (7) было положительным . Параметр b₂₁ может принимать значения [0, 1], если x₃ При . При . Многообразие параметров в формулах (7) и оптимизация поставленной задачи требует дополнительных условий. В качестве таких условий выберем , и . Первое неравенство означает, что , где , - величины сил упругости и демпфирования соответственно. Остальные задают условия для выбора коэффициентов

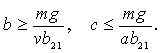(8)

Определим, удовлетворяют ли критерию оптимальности (5) полученные параметры в условиях (8). Для этого положим, например, и , тогда , и , . Подставим найденные значения в (5) имея ввиду максимальные значения переменных , где w - частота нагрузочного режима совпадающая с собственной частотой, получим два плана оптимальных решений из которых следует выбрать наилучший:

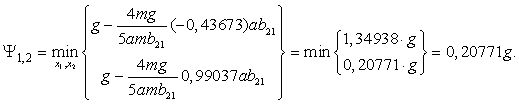(9)

В результате, наилучшим будет план , , соответствующий точке B на рисунке 1 а. Подставим найденные значения во вторую функцию состояния Y₃, задаваемую формулой (5)

, (10)

в которой оптимальный коэффициент упругости c, вычисленный по условию (8) будет составлять , коэффициент , наименьшее перемещение виброизолируемого объекта не будет превышать . В результате получим,

(11)

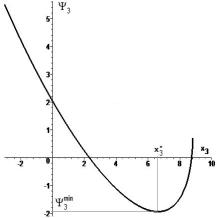
Локальный экстремум функции Y₃ составляет при , вычисляется численно. Его график представлен на рисунке 2 б в положительной полуплоскости x₃³0. Получен оптимальный план с параметрами: (м), (м/с), , при выбранных , , которому соответствует минимальное ускорение тела Y₃.

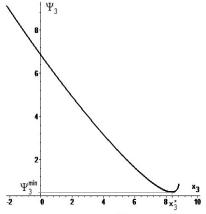
а) б) в)

Рисунок 1 - Пересечение эллипсоида работы сил сопротивления с плоскостью (x₁, x₂) на а, графики целевых функций Y₃ для разных коэффициентов упругости с на б и в

Заключение. Проведенные исследования позволяют сделать вывод о том, что с ростом коэффициента упругости пружины c виброамортизатора увеличивается по абсолютной величине оптимальное ускорение Y₃ изолируемого тела, уменьшается общая сила сопротивления mx₃* затуханию вредных колебательных режимов и рассеивание энергии.

Литература

1. Беллман Р., Калаба Р. Динамическое моделирование и современная теория управления. - М.: Наука, 1969.- 119 с.

2. Докукова Н.А., Кафтайкина Е.Н., Конон Н.П. Сравнительные характеристики пяти типов виброамортизаторов// Теоретическая и прикладная механика. Вып. 30: международный научно-технический сборник/ БНТУ.– Минск, 2015. Вып.–30.- С. 216-222.

3. Докукова Н.А., Голод С.В., Кафтайкина Е.Н. Исследование макета подвески сиденья транспортного средства// Теоретическая и прикладная механика. Вып. 29: МНТС / БНТУ.– Минск, 2014. Вып.–29.– С. 156-161.