Физика/7. Оптика

 

Сашкова Я. В., Одаренко Е.Н.

Харьковский национальный университет радиоэлектроники, Украина

Падение плоской волны на градиентную цилиндрическую линзу «РЫБИЙ ГЛАЗ» МАКСВЕЛЛА

 

Обычные линзы характеризуются однородным распределением коэффициента преломления по всему материалу, из которого они изготовлены. Используя законы Снеллиуса, можно сравнительно просто вычислять кусочно-линейные траектории лучей, проходящих через такие линзы. Материалы, относящиеся к типу GRIN (GRadient INdex), обладают градиентно-неоднородным распределением показателя преломления, благодаря чему лучи света распространяются в них по криволинейным траекториям. Существуют различные виды GRIN линз и законов изменения показателей преломления в них. Например, линзы Люнеберга, Итона-Липмана, Микаэляна и другие [1, 2]. В настоящее время довольно пристальное внимание исследователей сосредоточено на изучении линз типа «рыбий глаз» Максвелла (РГМ) в связи с предполагаемой возможностью преодоления дифракционного предела в формировании изображений [3, 4].  Показатель преломления такой линзы в полярной системе координат изменяется по закону:

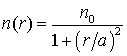,                                                      (1)

где n0  – показатель преломления в центре структуры;  – расстояние от центра линзы, на котором показатель преломления уменьшается в два раза.

В этой системе отсутствуют все аберрации, кроме дисторсии и кривизны поля изображения. Такая линза фокусирует каждую точку на сферической поверхности радиусом R в диаметрально противоположную точку на той же поверхности. В пределах линзы лучи проходят путь по дуге окружности.

 

Поскольку уникальные свойства РГМ линз можно использовать не только в оптическом, но и в терагерцовом и микроволновом диапазонах, то актуальными являются исследования электродинамических свойств различных конфигураций градиентных линз с пространственным распределением показателя преломления вида (1).

В данной работе рассматривается рассеяние плоской монохроматической волны на бесконечном диэлектрическом цилиндре с неоднородным распределением показателя преломления, характерным для РГМ линз. Непрерывное распределение  заменяется на кусочно-однородное путем представления цилиндра в виде многослойной структуры, т. е. неоднородная среда заменяется стратифицированной.

Рассматривается бесконечный диэлектрический многослойный цилиндр (количество слоев ) с произвольными материальными параметрами. Образующая цилиндра – координатная ось Оz. Показатель преломления сердцевины , показатель преломления слоев в общем случае разный (, где   – номер слоя). Вдоль положительного направления оси Оx на структуру падает электромагнитная монохроматическая волна с амплитудой  и параллельной поляризацией (вектор напряженности электрического поля параллелен образующей цилиндра). Компоненты поля в различных областях структуры обычно представляются в виде бесконечных рядов по цилиндрическим функциям:

·  Волна, падающая на цилиндр 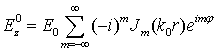                           (2)

·  Рассеянная цилиндром волна 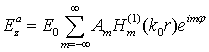                             (3)

·  Поле в сердцевине цилиндра 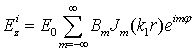                                 (4)

·  Поле внутри j-го слоя 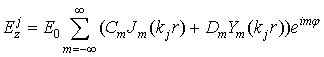               (5)

Здесь: – функция Бесселя первого рода; – функция Неймана;  – функция Ханкеля первого рода; , ,  – волновые числа окружающей среды, сердцевины цилиндра и -го слоя соответственно; , , ,  – амплитудные коэффициенты.

Применение граничных условий на границах раздела частичных областей в исследуемой структуре приводит к системе линейных уравнений, которую можно представить в матричном виде:

,                                             (6)

где  – матрица системы;  – вектор-столбец неизвестных коэффициентов;  – вектор-столбец правых частей неоднородной системы уравнений. Такая форма записи системы уравнений значительно упрощает процедуру ее решения с применением современных пакетов компьютерной алгебры. В данной работе использовался пакет MathCAD, в котором был создан  расчетный проект по визуализации пространственного распределения интенсивности электрического поля внутри и снаружи многослойного цилиндра. Проект позволяет проводить исследования для произвольного количества слоев структуры, их геометрических размеров и материальных параметров. Следует отметить, что показатели преломления слоев могут быть отрицательными, т.е. существует возможность исследования структур, содержащих метаматериалы.

На рис. 1 представлены результаты расчетов для однородной цилиндрической линзы с показателем преломления n = 1.5 и для неоднородной многослойной линзы, показатель преломления которой изменяется по закону (1). Отношение диаметра цилиндра к длине волны излучения D/λ = 3. Волна падает на цилиндр с левой стороны.

Сравнительный анализ полученных пространственных распределений интенсивности электрического поля показывает, что общий характер фокусировки излучения сохраняется при переходе от однородных линз к градиентным. Фокус образуется за цилиндром. Однако видны и довольно существенные отличия. В первую очередь, это наличие областей концентрации поля внутри многослойного цилиндра. В однородном цилиндре это явление практически отсутствует. Следует отметить также, что в данном случае градиентная цилиндрическая линза характеризуется более сильным отражением поля, что необходимо учитывать при проектировании устройств. Кроме того, область фокусировки градиентной линзы имеет более протяженный и локализованный в пространстве характер, что является ее важным преимуществом при использовании в устройствах для ввода излучения в волноводы.


Список источников

 


1.     Kay A. F. Spherically Symmetric Lenses // IRE Trans. On Antennas and Propagation. – 1959. – Vol. 7. – P. 32-38.

2.     Микаэлян А.Л. Применение слоистой среды для фокусирования волн // Доклады академии наук СССР. – 1951. – Т.81. – С. 569-573.

3.     Leonhardt U. Perfect imaging without negative refraction // New Journal of Physics. – 2009. – Vol. 11. – 0930140.

4.     Котляр В.В., Мелехин А.С. Расчет обобщенных линз «рыбий глаз» Максвелла и Итона-Липмана // Компьютерная оптика. – 2002. – №24. – С. 53-57.