Технические науки / 6.Электротехника и радиоэлектроника.

к.т.н. Боннет В.В., Прудников А.Ю.,

к.т.н. Потапов В.В., к.т.н. Черных А.Г.

Иркутский государственный аграрный университет, Россия

ОПРЕДЕЛЕНИЕ МАГНИТНОЙ ИНДУКЦИИ В ВОЗДУШНОМ ЗАЗОРЕ ПРИ ЭКСЦЕНТРИСИТЕТЕ АСИНХРОННОГО ДВИГАТЕЛЯ

Наличие эксцентриситета приводит к изменению индукции в воздушном зазоре, т.е. появлению магнитной асимметрии и, как следствие, к изменению электромагнитных и электрических величин и параметров, характеризующих работу асинхронного электродвигателя (АД), как электромеханического преобразователя [1].

В аналитических расчетах переходных и установившихся режимов АД с магнитной асимметрией наиболее часто применяется метод двух реакций или метод симметричных составляющих, позволяющий для соответствующей АД эквивалентной схеме замещения с сосредоточенными параметрами определить связанные с ней электрические величины (токи в обмотках двигателя).

Именно схемы замещения являются основным аппаратом для расчета электрических машин, в том числе и АД; их математическими моделями служат системы обыкновенных дифференциальных уравнений, описывающих процессы в схемах замещения и отражающими суть второго закона Кирхгофа для статорной и роторной цепей двигателя. Однако для расчета параметров схемы замещения соответствующей АД необходимо выполнить расчет электромагнитного поля в двигателе, т.е. решить систему уравнений математической физики в частных производных – уравнения Максвелла.

Решение полевой задачи, соответствующей расчету поля в поперечном сечении позволяет получить:

– радиальную составляющую напряженности статического магнитного поля в воздушном зазоре АД с синусоидальными токовыми слоями на статоре и роторе, когда обе поверхности являются гладкими концентрическими цилиндрами;

– элементы схем замещения магнитной и электрической цепи для идеального холостого хода и идеального короткого замыкания АД.

Необходимо отметить, что полученное решение удовлетворяет частному случаю, когда имеется магнитная неравномерность в воздушном зазоре, например, при эксцентриситете.

Кроме того использование лишь радиальной составляющей напряженности магнитного поля позволяет в дальнейших расчетах использовать понятие и соответствующей ей параметр получивший название в классической теории электрических машин намагничивающей (магнитодвижущей) силы (МДС) воздушного зазора взамен напряженности магнитного поля.

При использовании понятия результирующей МДС обмоток статора и ротора и магнитной проводимости зазора магнитная индукция в воздушном зазоре в точке с координатами x в момент времени t, в комплексной форме определяется выражением

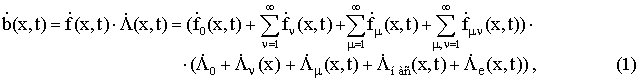
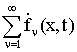где – комплекс магнитной индукции в воздушном зазоре; – комплекс м.д.с. обмоток статора и ротора; – комплекс магнитной проводимости зазора; – комплекс МДС основной волны; – комплекс МДС для пространственных гармоник статора; 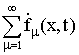– комплекс МДС для тока ротора с частотой s·f₁; 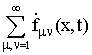– комплекс МДС пространственных гармоник создаваемых временными гармониками токов в проводниках ротора; – комплекс постоянной составляющей магнитной проводимости воздушного зазора; – комплекс относительной магнитной проницаемости при гладком роторе и зубчатом статоре; – комплекс относительной магнитной проницаемости при гладком статоре и зубчатом роторе; – комплекс относительной магнитной проницаемости, учитывающей явление насыщения; – комплекс относительной магнитной проницаемости при эксцентриситете.

Для практических расчетов должны быть приняты во внимание следующие парные произведения для МДС и проводимостей, входящие в выражение (1) и определяющие результирующее поле в воздушном зазоре двигателя:

1) 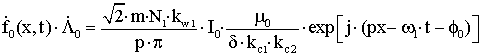– основное поле; f₀ – угол сдвига фаз в режиме холостого хода (см. рис. 1);

2) 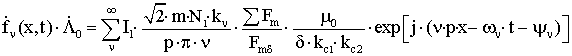– гармоники обмотки статора, имеющие фазу рабочего тока статора y_n=y₁ (см. рис.1), число пар полюсов и частоту гармоник МДС статора;

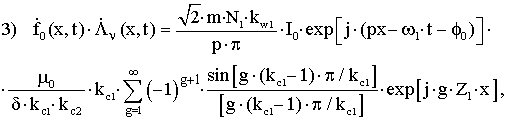
– гармоники, обусловленные зубчатостью статора;

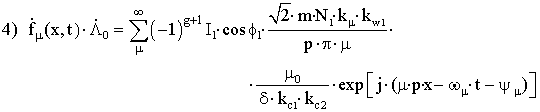
– гармоники обмотки короткозамкнутого ротора, имеющие фаз y_m=y₂ (см. рис.1), число пар полюсов и частоту гармоник МДС ротора;

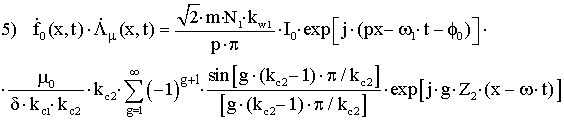
– гармоники, обусловленные зубчатостью ротора;

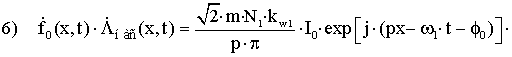
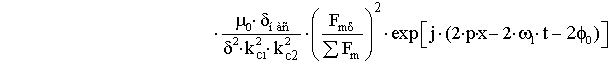
– гармоники, обусловленные явлением насыщения, создаваемые основным полем;

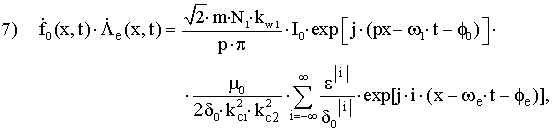
– гармоники, обусловленные эксцентриситетом, создаваемые основным полем; w_e=0 – в случае статического эксцентриситета; w_e=w=w₁·(1–s)/p – в случае динамического эксцентриситета; d₀=d.

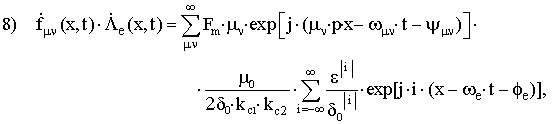
– гармоники, обусловленные эксцентриситетом, создаваемые токами в роторе.

Радиальные составляющие индукции в воздушном зазоре определяются действительной частью выражений в п.п. 1) ¸ 8) и имеют вид:

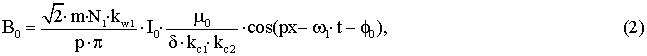
– для основной гармоники

– для пространственной гармоники статора с порядковым номером 2mq+1=2m+1 для (q=1); w_n=2m+1=w₁/(2mq+1)=w₁/(2m+1) для (q=1) вращающейся в направлении основной гармоники.

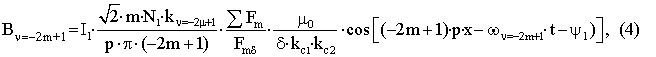
– для пространственной гармоники статора с порядковым номером 2mq+1=-2m+1 для (q=-1); w_n=2m+1=w₁/(2mq+1)=w₁/(-2m+1) для (q=-1), вращающейся против направления вращения основной гармоники.

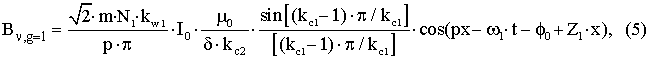– для пространственной гармоники, обусловленной зубчатостью статора с порядковым номером g=1.

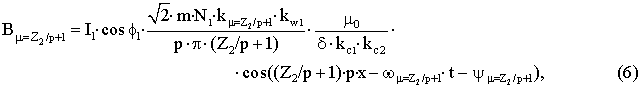
– для пространственной гармоники ротора с порядковым номером (qZ₂/p)+1=Z₂/p+1 и w_m=Z2/p+1=w₁/[(qZ₂/p)·(1–s) +1=w₁/[(Z₂/p)·(1–s) +1] для (q=1) вращающейся в направлении вращения ротора; y_m=Z2/p+1=f₁+arctan(I₀·s_н/I_к·s).

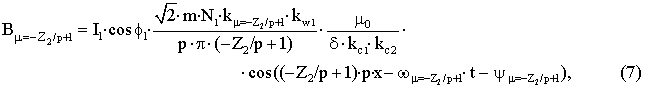
– для пространственной гармоники ротора с порядковым номером (qZ₂/p)+1=–Z₂/p+1 для (q=–1); w_m=Z2/p+1=w₁/[(qZ₂/p)·(1–s) +1=w₁/[(–Z₂/p)·(1–s) +1] для (q=–1) вращающейся против направления вращения ротора; y_m=–Z2/p+1=f₁+arctan(I₀·s_н/I_к·s).

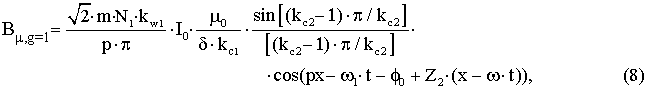
– для пространственной гармоники, обусловленной зубчатостью ротора с порядковым номером g=1.

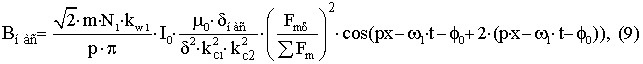
– для пространственной гармоники, учитывающей явление насыщения; d_нас –_{увеличенный виртуальный воздушный зазор, позволяющий учитывать явление насыщения.}

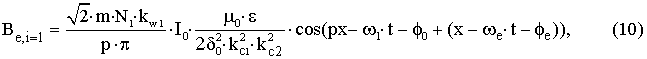
– для пространственной гармоники учитывающей эксцентриситет с порядковым номером i=1 вращающейся в направлении основной гармоники.

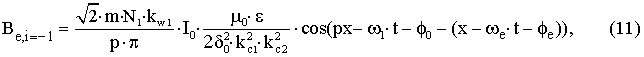
– для пространственной гармоники учитывающей эксцентриситет с порядковым номером i=–1 вращающейся против направления вращения основной гармоники.

Выражения (10) и (11) могут быть объединены в единое уравнение (12) с учетом следующих введенных обозначений:

– n_e=1±1/p; w_ne=w₁±w_e; f_ne=f₀±f_e.

Для нахождения произведения по выражению п.п. 8) необходимо внести следующие уточнения: i=±1; n=2mq+1; q=±1; m_n=q·Z₂/p+n – принимает следующие значения: m_n,q=1,n=2m+1=Z₂/p+2m+1, m_{n,q=–1,n=2m+1}=–Z₂/p+2m+1, m_{n,q=1,n=–2m+1}=Z₂/p–2m+1, m_{n,q=–1,n=–2m+1}=–Z₂/p–2m+1; w_mn=w₁·[(q·Z₂/p)·(1–s)+1] – принимает следующие значения: w_{mn, q=1}=w₁·[(Z₂/p)·(1–s)+1], w_{mn, q=–1}=w₁·[(–Z₂/p)·(1–s)+1].

Таким образом, произведения по выражению п.п. 8) примут вид

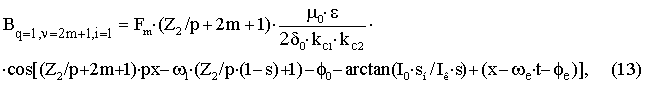
– для пространственной гармоники ротора с порядковым номером Z₂/p+2m+1 учитывающей эксцентриситет с порядковым номером i=1 вращающейся в направлении основной гармоники.

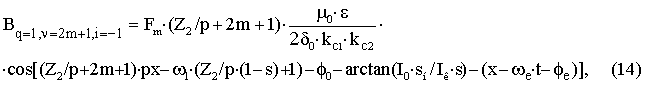
– для пространственной гармоники ротора с порядковым номером Z₂/p+2m+1 учитывающей эксцентриситет с порядковым номером i=–1 вращающейся против направления вращения основной гармоники.

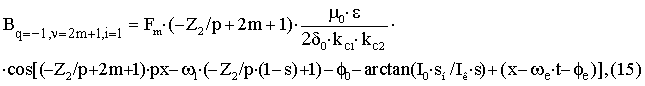
– для пространственной гармоники ротора с порядковым номером –Z₂/p+2m+1 учитывающей эксцентриситет с порядковым номером i=1вращающейся в направлении основной гармоники.

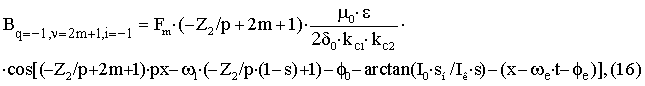
– для пространственной гармоники ротора с порядковым номером –Z₂/p+2m+1 учитывающей эксцентриситет с порядковым номером i=–1вращающейся против направления вращения основной гармоники.

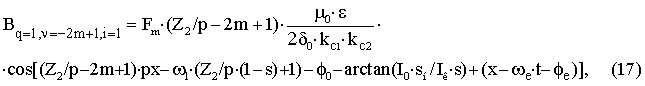
– для пространственной гармоники ротора с порядковым номером Z₂/p–2m+1 учитывающей эксцентриситет с порядковым номером i=1вращающейся в направлении основной гармоники.

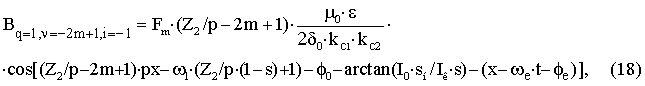
– для пространственной гармоники ротора с порядковым номером Z₂/p–2m+1 учитывающей эксцентриситет с порядковым номером i=–1вращающейся против направления вращения основной гармоники.

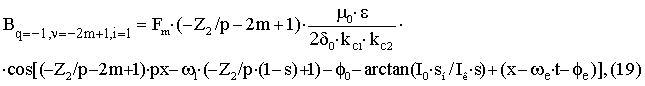
– для пространственной гармоники ротора с порядковым номером –Z₂/p–2m+1учитывающей эксцентриситет с порядковым номером i=1вращающейся в направлении основной гармоники.

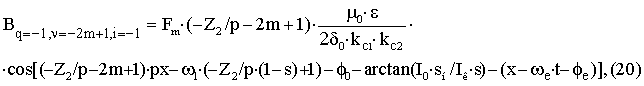
– для пространственной гармоники ротора с порядковым номером –Z₂/p–2m+1учитывающей эксцентриситет с порядковым номером i=–1вращающейся против направления вращения основной гармоники.

Литература:

1. Генкин М.Д., Соколова А.Г. Виброакустическая диагностика машин и

механизмов. М: Машиностроение, 1987.

2. Шубов И.Г. Шум и вибрация электрических машин / И.Г. Шубов – Л: Энергоатомиздат, 1986.

3. Шуйский В.П. Расчет электрических машин / В.П. Шуйский – Л: Энергия, 1968.