Технические науки/Электротехника и радиоэлектроника

Профессор Алиев И.И.

Северокавказская государственная гуманитарно-технологическая академия

Математическое моделирование и определение

коэффициента мощности асинхронного энергосберегающего

двигателя

Автором ранее были представлены некоторые результаты экспериментального исследования асинхронного энергосберегающего двигателя (АЭД) [1], защищенного свидетельством РФ на полезную модель [2]. Было показано, что АЭД можно представить как совмещенную электрическую машину, включающую АД с короткозамкнутым ротором и вспомогательный синхронный генератор с небольшими постоянными магнитами на роторе, занимающую промежуточное положение между двумя этими типами машин. Экспериментальный АЭД на базе двигателя типа 4АИС56В2 обеспечивал снижение потребляемой из сети реактивной мощности до 25-30%, в сравнении с серийным АД, и соответствующее увеличение коэффициента мощности.

Ниже приводится некоторые результаты исследования АЭД методом математического моделирования. Математическая модель разработана при общепринятых допущениях, представлены результаты расчета реактивных мощностей и коэффициентов мощности для АЭД на базе серийных многополюсных асинхронных двигателей. Последние отличаются, как известно, невысоким коэффициентом мощности.

Проблема расчета энергии постоянных магнитов (ПМ) рассмотрена, например, в работе [3]. Получено простое соотношение для определения объема (или энергии) ПМ, используемое при построении математической модели АЭД:

V = Q/ 2Wf ω(1 - s). (1)

где Q- реактивная мощность фазы; W - удельная энергия ПМ; f - частота напряжения статора, ω- синхронная скорость, s - скольжение двигателя.

Для асинхронных двигателей с числом полюсов 8-12 были выполнены расчеты объемов магнитов на фазу. При моделировании ПМ использовались параметры сплава ЮНДК35Т, имеющего В = 0,8 Тл и Н = 87 А/м. Например, для двигателя АИР180МВ12 объем ПМ составил 11,6 см, а мощность ПМ - 29 вар при реактивной мощности фазы 2948 вар. Для получения объема ПМ на всю машину, это значение следует утроить. Мощность ПМ в среднем в 10 раз меньше реактивной мощности фазы. Это объясняется практически линейной зависимостью эквивалентной мощности ПМ от скорости их вращения [3].

Математическая модель АЭД при общепринятых допущениях имеет вид:

Уравнения напряжений обмоток статора и ротора:

U = Ri + ψ/dt - ω ψ ,

U = Ri + ψ/dt - ω ψ, (2)

0 = Ri+ ψ/dt,

0 = Ri+ ψ/dt;

уравнения потокосцеплений:

ψ = xi + xi + e,

ψ = xi + xi, (3)

ψ = xi + xi+ e,

ψ = xi + xi;

уравнение движения ротора:

(J/p)/ d ω/dt = M - М. (4)

В уравнениях (2-4) помимо общеизвестных величин напряжений, токов, активных и индуктивных сопротивлений статора и ротора, имеется эквивалентная ЭДС постоянных магнитов e. Она определяется соотношением:

e = (е/) е/RG, (5)

где: е- базисная ЭДС, е - ордината пересечения прямой возврата магнита с характеристикой холостого хода, R - магнитное сопротивление воздушного зазора, G - суммарная магнитная проводимость постоянного магнита.

Базисная ЭДС езависит от числа витков статора w , частоты напряжения f, рабочего магнитного потока Ф, обмоточного коэффициента обмотки статор k, коэффициента формы поля k:

е= 2πf w k Ф/ k. (6)

Решение дифференциальных уравнений после их соответствующей подготовки осуществлено на ПК в программной среде МАСС (машинный анализ и синтез систем).

В результате моделирования получены временные зависимости частоты вращения ротора, величины электромагнитных моментов, токов статора и ротора в процессе пуска АЭД и в установившемся режиме. Ограничимся здесь анализом важнейшего энергетического параметра двигателей - коэффициента мощности.

На рис.1 для наглядности приведена осциллограмма напряжения и тока фазы АЭД на базе двигателя 5АМ250S8 мощностью 37 кВт с ПМ на роторе, объем которых равен V = 22,5 см³ на фазу. Коэффициент мощности этого АЭД в номинальном режиме составляет сosφ = 0,84, чему соответствует потребляемая реактивная мощность 23, 8 квар, тогда как у базового двигателя эти величины равны соответственно сosφ = 0,72 и Q =25,6 квар.

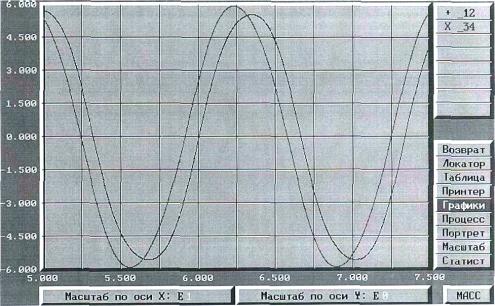
Рис.1. Кривые напряжения и тока АЭД на базе двигателя 5АМ250S8 (объем постоянных магнитов на роторе V = 22,5 см³, сosφ = 0,84)

Если увеличить объем магнитов этой же машины до величины V = 59,5 см³, то коэффициент мощности АЭД составит сosφ = 0,927, а потребляемая реактивная мощность - лишь 15 квар.

Были выполнены расчеты АЭД на базе двигателя АИР180МВ12 мощностью 12,9 кВт с ПМ на роторе объемом V= 19,2 см³. Его коэффициент мощности сosφ = 0,812, тогда как коэффициент мощности серийного двигателя сosφ = 0,678. Соответственно, реактивная мощность для АЭД равна 9,25 квар, а для базового -13,98 квар, т.е её потребление снижается на 34%.

Известно, коэффициент мощности машин тем меньше, чем меньше их синхронная скорость, т.е. чем больше число пар полюсов. Расчеты показывают, что применение магнитов тем эффективнее, чем больше полюсов у базового двигателя.

Вывод. Качественное сравнение данных, полученных теоретическим путем, с экспериментальными результатами, показывает, что применение небольших постоянных магнитов на роторе асинхронного энергосберегающего двигателя позволяет существенно увеличить его коэффициент мощности в сравнении с серийной машиной той же мощности, снизить потребление реактивной мощности, разгрузить сети от реактивных токов и обеспечить тем самым значительную экономию электроэнергии.

Литература

1. Алиев И.И. Асинхронный энергосберегающий двигатель. Электротехника, 2001, №11, с.39-41.

2. Свидетельство РФ на полезную модель №17751. Асинхронный двигатель/ И.И. Алиев //Открытия. Изобретения. 2001, № 11.

3. Aliev I., Bespalov V. Asynchronous generator with guaranteed self-excitation. 5^th International conference "Unconventional electromechanicall and electrical systems", Poland, - Szczecin: TU-Press. 2001. Volume 2 - p.p. 209-212.