Современные информационные технологии /1. Компьютерная инженерия

Аждер В.Д., Потапова М.С.

Московский технологический университет, Россия

Анализ методов решения задачи прогнозирования

Рассмотрим задачу прогнозирования, когда необходимо одновременно учитывать погрешности в значениях функции и в значениях аргументов.

Пусть требуется найти интервальную оценку параметра функции , причем точные значения и наблюдать нельзя, а значения случайных величин и можно. и определяются следующим образом:

x_i=ξ_i+δ_i ; y_i= η_i + ε_i , i=1,2,…,n,

где δ_i и ε_i – соответственно ошибки значений переменных и функции.

Пусть имеем статистический ряд экспериментальных значений {x_i}X и соответствующий им ряд значений функций {y_i}Y, i=1,2,…,n, n≥m, где m – число оцениваемых параметров .

Найдем выражение для совместной плотности вероятности экспериментальных данных. Значения ξ_i и η_i связаны функциональной зависимостью, их погрешности δ_i и ε_i являются независимыми при переходе от одной точки (x_i , y_i) к другой. Тогда совместная плотность вероятности случайного события получить одновременно значения x_i и y_i имеет вид:

,

где – функция математического ожидания ξ_i,

– функция математического ожидания η_i.

Совместная плотность вероятности для получения n статистически независимых точек (x_i , y_i) вычисляется по формуле

.

Функциональное соотношение , (1)

порождает структурное соотношение между наблюдаемыми случайными величинами x_i и y_i: , или

при аддитивных помехах δ_i , ε_i .

Пусть экспериментальные значения x_i и y_i – случайные величины, каждая из которых имеет функцию плотности вероятности, описываемую функцией Гаусса с математическими ожиданиями ξ_i и η_i, дисперсиями σ²(x_i), σ²(y_i) и коэффициентом корреляции ρ_i=ρ(x_i,y_i). Плотность вероятности получить точку с координатами (x_i , y_i) вычисляется по формуле

,

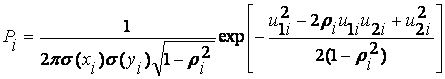где ; .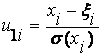

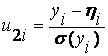Совместная плотность вероятности получить n независимых таких точек имеет вид и

lnL(X,Y)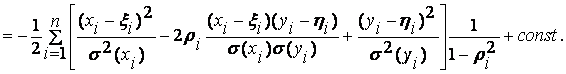

Оценки искомых параметров находятся из условия минимума функционала

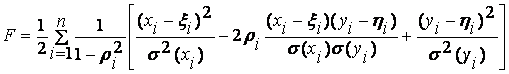. (2)

Если погрешности δ_i и ε_i некоррелированы, то выражение (2) примет вид:

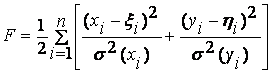. (3)

Перед определением точки минимума функции (2) по необходимо определить ξ_i . Искомые значения ξ_i и оценки определяются из условия

, .

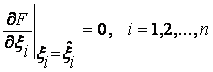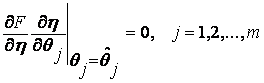Таким образом, решение задачи минимизации функционала (2) эквивалентно решению системы уравнений

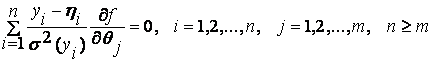(4)

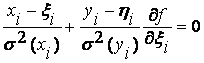при (5)

Для функций, линейных по параметрам , система уравнений (3) – это система линейных алгебраических уравнений. Замена нормального закона распределения другим, приводит к системе нелинейных уравнений (4).

В задаче прогнозирования при одновременном учете погрешности в значениях функции и в значениях аргументов классический метод наименьших квадратов не так точен, как метод, основывается на конфлюэнтном анализе.

Литература:

1. Грешилов А.А., Стакун В.А., Стакун А.А. Математические методы построения прогнозов. – М.: Радио и связь, 1997.

2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник/ Под ред. чл.-корр. РАН И.И. Елисеевой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2001.

3. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. – 7-е изд. – М.: ФИЗМАТЛИТ, 2004.