А.Б. Хачатурян

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ», Россия

Ансамбли кодовых сигнатур укороченных минимаксных последовательностей

По мере насыщения выделенных участков спектра новыми глобальными спутниковыми навигационными системами (ГНСС) все острее становится проблема их бесконфликтного сосуществования как между собой, так и с соседствующими в эфире системами иного назначения. Для ГНСС ГЛОНАСС этот фактор оказывается критическим в связи с возможностью просачивания ее сигналов в примыкающий диапазон радиоастрономических наблюдений 1610.6…1613.8 МГц. Как показано в [4] указанная проблема может быть решена за счет использования спектрально-эффективных модуляционных форматов. Так модуляция с непрерывной фазой (МНФ), позволяет существенно сузить занимаемую полосу, не нарушив постоянства амплитуды сигнала. С учетом жесткой спектральной регламентации МНФ форматы предпочтительны по сравнению с БФМ с точки зрения таких ключевых показателей как фильтрация помехи множественного доступа (ПМД), точность временнóй привязки, точности измерении запаздывания сигнала, искаженного многолучевой помехой и др. Платой за полученные преимущества выступает, в том числе, необходимость укорочения кодовых последовательностей, используемых в широкополосных системах. В работе [4] предложен метод поиска ансамбля укороченных сигнатур объема 50 и длины последовательности 4092. Наилучшие корреляционные характеристики обеспечивали укороченные минимаксные последовательности Касами и Кердока. Ансамбль оригинальных последовательностей Касами длины 4095 содержит всего 64 сигнатуры. Статья посвящена методике построения ансамбля сигнатур длины и объемом с использованием минимаксных последовательностей и демонстрацией его иммунитета к ПМД.

Анализ электромагнитной совместимости модернизированных сигналов ГНСС с соседствующими службами в [4], показал, что в качестве ансамбля сигнатур необходимо использовать минимаксные последовательности длины и объемом . Поскольку среди известных минимаксных последовательностей нет кандидатов необходимой длины, было предложено использовать укороченные ансамбли минимаксных последовательностей, обеспечивающих наилучшие корреляционные характеристики.

Превосходство одного ансамбля над другим определяется величиной, называемой в системах CDMA помехой множественного доступа. ПМД , характеризует степень сходства -го и -го сигналов, смещенных друг относительно друга на позиций по времени и на Гц по частоте и имеет вид [2]

,

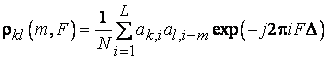где - длина дальномерного кода, , - длина одиночного импульса (чипа). Физически ПМД выражает нормированный отклик фильтра согласованного с -м сигналом на -й, расстроенный на Гц.

Поиск сигнатур модернизированного дальномерного сигнала состоит из следующих процедур: формируется оригинальный минимаксный ансамбль длины и объемом ; далее, прямоугольник размером перемещается по строкам и столбцам оригинального массива с расчетом максимального пика взаимной корреляции сигнатур, входящих в прямоугольник. Полученное в результате процедуры положение прямоугольника отвечает наименьшей величине максимального пика взаимной корреляции сигнатур, входящих в ансамбль. Процедуре подверглись следующие ансамбли [5–7]:

1. Ансамбль Голда ,

2. Объединенный ансамбль Касами и бент - последовательностей , ;

3. Ансамбль Кердока , .

Оригинальный ансамбль Касами содержит только 64 сигнатуры. Тем не менее, при его объединении с ансамблем бент - последовательностей с параметрами , , можно получить ансамбль большего объема, не содержащий циклических реплик и обеспечивающий прежний уровень ПМД. Следующий раздел посвящен анализу корреляционные характеристик представленных ансамблей, после процедуры поиска.

Как было сказано ранее, превосходство одного ансамбля над другим определяется величиной, называемой в системах CDMA помехой множественного доступа. ПМД , характеризует степень сходства -го и -го сигналов, смещенных друг относительно друга на с по времени и на Гц по частоте. Сравнение качественных показателей различных ансамблей производятся на основе следующих параметров:

1. максимального пика ПМД, определяемого как

,

2. среднеквадратического значения ПМД

,

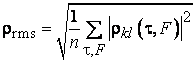где n – обозначает число различных кодовых пар в ансамбле

3. однопроцентный квантиль, определяемый как

уровень ПМД, вероятность которого не превышает 0,01. Поскольку реальный период повторения дальномерного сигнала составляет 1 мс, численный анализ ПМД показал, что увеличение доплеровского сдвига более чем на 5 кГц не приводит к его существенным изменениям. Следовательно, анализ следует проводить для двух вариантов: отсутствия частотного сдвига и частотного сдвига кГц. Результаты анализа укороченных кодовых последовательностей для этих зон сведены в таблицу 1.

Таблица 1

Минимаксный ансамбль
	ρmax, дБ	ρrms, дБ	ρ0.01, дБ	ρmax, дБ	ρrms, дБ	ρ0.01, дБ
Голд	-22.24	-36.29	-28.59	-22.24	-36.14	-28.59
Касами - бент	-22.99	-36.62	-32.92	-22.99	-36.62	-32.96
Кердока	-23.61	-36.66	-32.96	-23.61	-36.63	-32.96

Из результатов таблицы 1 видно, что доплеровская расстройка практически не влияет на значения корреляционных параметров сигнатур; среднеквадратическое значение корреляционно пика практически не зависит от типа ансамбля, а определяется его длиной (как и было теоретически предсказано [3]); ансамбль Кердока обеспечивает минимальное значения корреляционного пика с возможность увеличить количество сигнатур в 2 раза.

Литература:

1. J. Proakis, M. Salehi, Digital communication, 5th ed., MCGraw- Hill, 2007.

2. B. Sklar Digital communication: Fundumentals and applications. 2nd ed., Prentice Hall, 2001.

3. V.P. Ipatov. Spread spectrum and CDMA: Principles and aplications, Wiley, 2005.

4. A. B. Khachaturian, A.S. Mikheev, V. M. Kutuzov. “Proposals of compact spectrum CDMA signatures for the future GNSS air intrface”, IEEE ElConvRusNW, 2016, pp.231-232.

5. R. Gold, “Optimal binary sequences for spread spectrum multiplexing”, IEEE Trans. on Information Theory, v.13, iss.4, 1967, pp.619-621. A.B. Khachaturian, D.V. Gayvoronsky, “Delay estimation and multipath resistance potential accuracy of continuous phase modulation signals”, IET Communications, 2015.

6. F. Cheng, J. Hua, et al. “A fast generation ,ethod of bent sequences and its application in ADS simulation”, pp.328-331.

7. A.A. Nechaev, “Kerdock code in a cyclic form”, Discr. Math. Appl., v.1, №4, 1991, pp.365-384.