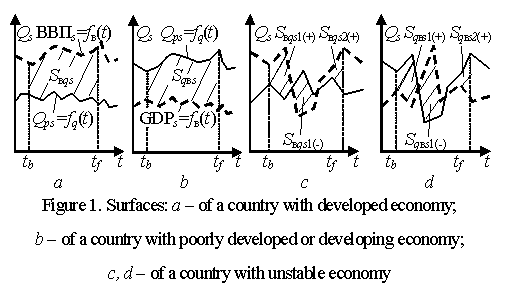
Classification
of countries according to surfaces occupied by the economy and population
Now let us introduce two groups of parameters that will be able to
characterize the processes taking place in regions, countries and in the whole
world more fully. This section uses common abbreviations, i.e. GDP instead of et,
as well as Qp instead of pt, which naturally
eases their reading.
1. Statistical parameters:
·
SGDPs is the
statistical surface occupied by the built-up
economic curve GDPs = fâ(t) within the time
period from tb to tf.. Unit2;
·
Sqps is the
statistical surface occupied by the built-up
economic curve of population Qps = fq(t) within
the time period from tb to
tf. Unit2;
·
Sâqs is the difference between statistical surfaces Sââïs and Sqps within
the time period from tb to
tf, when the built-up curve GDP = fâ(t) is placed
above the built-up curve Qps =
fq(t), i.e. all the values of GDPs > Qp. Unit2 (Figure 1a, 1b);
·
Sqâs is the
difference between statistical surfaces Sqps and Sââïs within the time
period from tb to tf, when the built-up curve Qps = fq(t) is placed above the built-up curve GDPs = fâ(t), i.e. all the values of Qps > GDPs. Unit2 (Figure 1c, 1d);
In this
section we adopted the symbols «â» and «q» in
descriptions of the curves GDPs =
fâ(t) and Qps = fq(t),
as well as of the formulas below in order to tell the difference in these
formulas between the values of fâ(t) and fq(t).
We can
similarly designate calculated parameters of both GDPc and population Qpc. Calculated parameters of GDPc and Qpc are understood to be parameters that were deduced by calculation on the
basis of developed formulas for forecasting respective values.
2. Calculated parameters:
·
SGDPc is the
calculated surface occupied by the built-up economic
curve GDPc within
the time period from tb to
tf. Unit2;
·
Sqpc is the calculated surface occupied by the
built-up economic curve of population
Qpc within
the time period from tb to
tf.Unit2;
·
Sâqc is the difference between calculated surfaces SGDPc and Sqpc within
the time period from tb to
tf, where GDPc > Qpc. Unit2;
·
Sqâc is the
difference between calculated surfaces Sqpc and SGDPc within the time
period from tb to tf, where Qpc > GDPc. Unit2.
Taking Figure 1 as reference, we can divide all countries into
the following four classes:
·
the class of highly-developed
industrial countries, where the statistical and calculated values of the
parameters will be the following: GDPs > Qps and GDPc
> Qpc respectively;
·
the class of poor, poorly
developed and developing countries, where the statistical and calculated values
of the parameters will be the following: Qps > GDPs
and Qpc > GDPc
respectively;
·
the class of countries with
unstable economy, where there are surfaces with negative statistical Sâqs1(-) and Sqâs1(-) (Figure 1c, d)
and respective calculated values of the parameters Sâqc1(-) and Sqâc1(-);
·
the class of transition period
countries, where the difference of surface sums SSâqsi and SSqâsj built on the basis of statistical data are equal to zero, i.e. SSâqsi – SSqâsj = 0.
These are
graphs where the built-up theoretical curves et and pt,
as well as built-up
statistical curves GDPs
and Qps will merge. The values of surfaces Sâqs = Sqâs = 0 and Sâqc = Sqâc = 0 are special cases, thus it is desirable to admit that the class of
transition period countries can include, for example, a country whose value of
surface S = fâ(t) differs from values of surface Sqps = fq(t) by ±5%.
Here we should
mention right away that calculated values of parameters may differ from the
statistic ones, if the deduced coefficients of correlation R2 for them are quite small. So, variant where
statistical parameters are the following: GDPs > Qps, and the calculated ones for them are Qpc > GDPc is possible.
Here:
·
SGDPs is the surface
occupied by the curve built-up on the basis of statistical values of GDPs within the time period from
tb to tf. Unit2;
·
Sqps is the
surface occupied by the curve built-up on the basis of statistical values of
population Qps
within the time period from tb to tf. Unit2;
·
Sâqc is the difference between the built-up surfaces SGDPs and Sqps
within the time period from tb to tf.,
where GDPs.> Qps. Unit2;
·
Sqps is the
difference between the calculated surfaces SGDPs
and Sqps
within the time period tb and tf,
where Qps > GDPs.
Unit2;
Statistic
values of GDPs and Qps are understood to be
such values when they are taken from official sources. Introduction of
parameters of statistical surfaces SGDPs and Sqps allow us to analyze more fully the state of the economy and population
of a country within a time period in question. Thus, for example, surface SGDPs will characterize wealth of the country’s population within a time
period in question. In its turn, the value of statistical surface of population
Sqps shows the change tendency of the country’s population within a time
period in question.
Moreover, we
should highlight that in time poorly developed countries may be included into
the class of developed countries. However, here we should specify right away
that developed countries will refer to countries with developed industry and
knowledge-intensive production.
A number of
rich countries, for example, the Persian Gulf countries, whose economic
prosperity is high due to oil and gas recovered, cannot be attributed to
highly-developed countries. For countries with developed economy the
statistical surface Sâqs is calculated according to the formula (1)
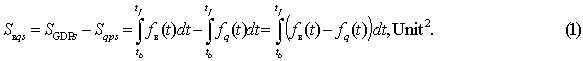
To calculate
the surface Spâs for poorly developed and developing countries we should use the formula
(2)
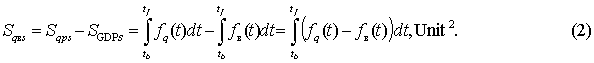
If we consider
countries with unstable economy, in this case we should use the following two
formulas (3) and (4) depending on specific conditions.
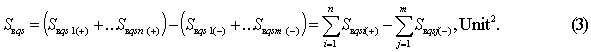
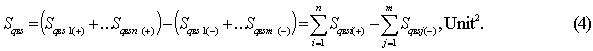
Here we shall
remark right away that the variants shown in Figure 1c and 1d may have specific cases where the sum
of positive surfaces 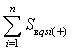
![]() will be equal to the sum of negative surfaces
will be equal to the sum of negative surfaces 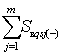
![]() , i.e.
, i.e. ![]()
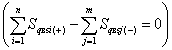 . However, these variants will
not be attributed to equilibrium variants, although the difference between
these sums will equal to zero.
. However, these variants will
not be attributed to equilibrium variants, although the difference between
these sums will equal to zero.