Kryuchin O.V., Kryuchin E.I.
Tambov State University named after G.R. Derzhavin, Russia
Adaptive resonance theory
and its second structure implementation using artificial neural network
As
we know one of the main problems which are solved by adaptive resonance theory
(ART) is the classification. There are different implementation method of this
theory and the best is the artificial neural networks (ANN). The primary intuition behind the ART
model of ANN is that object identification and recognition generally occur as a
result of the interaction of “top-down” observer expectations with “bottom-up”
sensory information. The model postulates that “top-down” expectations take the
form of a memory template or prototype that is then compared with the actual
features of an object as detected by the senses. This comparison gives rise to
a measure of category belonging. As long as this difference between sensation
and expectation does not exceed a set threshold called the “vigilance
parameter”, the sensed object will be considered a member of the expected class
[1].
The basic ART
system is an unsupervised learning model. It typically consists of a comparison
field and a recognition field composed of neurons, a vigilance parameter, and a
reset module. To
date only few types of ART networks have been developed. These networks
self-organize stable recognition categories in response to arbitrary sequences
of analog input patterns, as well as binary input patterns. Computer
simulations are used to illustrate the dynamics of the system [2].
ART
networks consist of two layers. These are the input layer of the comparating
which has L neurons and the output
layer of the clarication which has P neurons. Each neuron of
it the input layer is connected to each neuron of the output layer using
ascendant synaptic links (
),
and each neuron of the output layer is connected to each neuron of the input
layer using descending links (
)
[3]. The ART-2 structure
specificity is the availability of six sublayers in the input layer. Each
sublayer consists of L neurons. The availability of these sublayers is
conditional upon necessity for the normalization of input values. Example of
such structure is shown in Figure 2. This network has fifty seven neurons in
sublayers of the input layer (are shown using the blue-cyan color) and fifteen
neurons in the output layer (are shown using the purple-red color) (L=57,
P=15). The input values of this network are vectors 
which are given serially. Each vector 
has L elements 
.
The ART-2 network
has few parameters:
·
The
threshold of the aboutness 
. This is the real
number which lies in the band (0; 1). If this value is near zero then the
requirement of aboutness is faithful.
·
Coefficients
, 
and 
. These are numbers
which are greater then zero. They are needed for the function minimization.
·
The
coefficient 
which is the small real number. It is greater
then zero and is needed for the keeping from the division by zero.
·
The
small real number 
which is the criterion of the truncation of
the noise. This truncation uses formula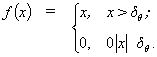 
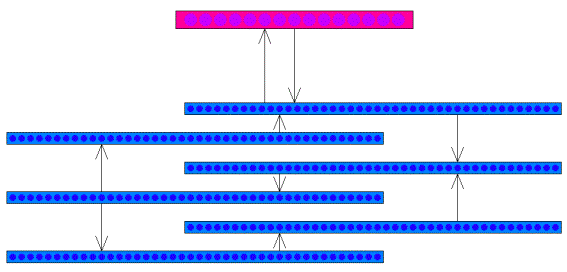
Figure 1. The detailed structure of ART-2 network.
In the beginning
training ANN it has L neurons in each sublayer of the input layer and
one neuron in the output layer. Weights of links are initialized by formulas 
and hat 
for each i-th neuron.
The condition of
all neurons in sublayers of the input layer are zero. When new vector 
is given then it executes few operation:
1.
All
neurons of the output layer are actuated.
- Values of neurons in sublayers of the input layer
are calculated serially by formulas
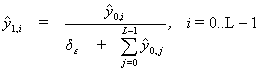
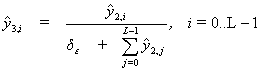
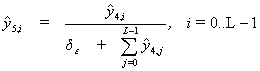
where 
is the vector of input signals, 
is the vector of values of the k-th
sublayer of the input layer.
3.
Values
of neurons of the output layer are calculated by formula 
(for each neuron of the output layer).
4.
If
there are active neurons then it selects the neuron having the maximal value
(the neuron-champion) and enumerates values of neurons of the input layers by
formula 
where 
is the index of the neuron-champion.
Then it checks the aboutness of the
neuron-champion by formula 
where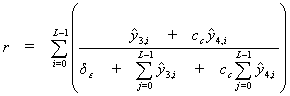 
.
If the assumption 
is executed then it corrects weight
coefficients of the neuron-champion are updated else it disactivates the
neuron-champion and selects new champion from other active neurons. If there
are not active neurons then it generates new output neuron (new class is
created) with weights calculating by formulas where i=0....L-1.
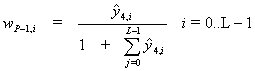
The result of the
ANN work is the index of the neuron having the maximal value (
) which was checked
on the aboutness. The image was associated to the acquainted class (claster) of
objects. Or the information about necessity for the creating new class (the
class for the current vector is absent).
Literature
1.
O'Meadhra, C.E.; Kenny, A.: Sensory Modal Switching.
Discussion Paper, Multisensory Design Research Group at the National College of
Art and Design 2011
2.
Carpenter G.A., Grossberg S. ART 2: Self-organization
of stable category recognition codes for analog input patterns // Applied
Optics, 26(23), 1987. P. 4919-4930.
3.
Grossberg S. Competitive learning: from interactive
activation to adaptive resonance // CognitiveSci. 11, 23(1987).