Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

Захарук Р.П.

Прикарпатський національний університет імені В.Стефаника

Варіація методу малого параметру розв’язання задачі Коші для гіперболічної системи двох квазілінійних рівнянь першого порядку

Розглянемо задачу Коші для системи двох квазілінійних рівнянь з частинними похідними першого порядку    

   (1)

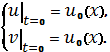(2)

Нехай функції потоку двічі неперервно диференційовні, а початкові функції - обмежені вимірні функції.

Вважаємо, що система рівнянь (1) гіперболічна, а саме, що матриця

(3)

має два дійсних різних власних значення , і, крім того, система рівнянь (1) сильно нелінійна у тому сенсі, що

(4)

де - праві власні вектори матриці (3).

Нехай функція опукла вниз (для функції це забезпечується, наприклад, умовою ), а пара функцій задовольняє матричне рівняння

. (5)

Разом із задачею (1), (2) розглянемо її збурення за методом в’язкості, а саме, задачу Коші для системи двох параболічних рівнянь з частинними похідними другого порядку 

   (6)

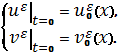(7)

Означення Пара обмежених вимірних функцій називається узагальненим розв’язком задачі (1),(2), якщо справджуються інтегральні тотожності

(8.1)

(8.2)

інтегральна нерівність

(9)

та початкові умови (2) приймаються у слабкому сенсі.

Теорема Нехай класичний розв’язок задачі (6), (7) апроксимує вектор-функцію в . Тоді – узагальнений розв’язок задачі (1), (2).

Доведення Діючи за схемою, викладеною в [2], до першого рівняння системи (6), помноженого на додамо друге, помножене на , і далі результат проінтегруємо по . Скористаємося теоремою Остроградського, а далі фінітністю пробної функції і умовою (5) , отримаємо

,

і переходячи в цій нерівності до границі при , в результаті отримаємо нерівність (9). Якщо ж застосувати теорему Остроградського до проінтегрованого рівняння (1) або (2), помноженого на , отримаємо інтегральні тотожності (8.1), (8.2). Якщо ж в рівностях (8.1), (8.2) пробну функцію вибрати так, щоб її носій містився в малому околі початкової прямої , то в граничному випадку отримаємо слабке прийняття початкових умов з функціями =

Для того, щоб скористатися теоремою, було побудовано розв’язки задачі

(6), (7) у вигляді степеневих рядів для системи з поліноміальними потоковими функціями і простішими початковими аналітичними функціями. Обчислення було проведено за допомогою математичного пакету Maple. Отримані наближення узагальненого розв’язку задачі (1), (2) проаналізовано за допомогою графічної візуалізації в Maple.

Зауважимо, що запропонований метод є досить ефективним при аналізі також і задачі Рімана, і задачі про розпад розриву.

Література:

1. Lax P.D. Hyperbolic system of conservation laws.-Comm. Pure Appl.Math.-1957.-V.10.-p.537-566.

2. Казмерчук А.І. До обґрунтування наближених методів розв’язання квазілінійних законів збереження з негладкими даними задачі. - Вісник національного університету “Львівська політехніка”, Прикладна математика.-2000.-№411.-с.147-151