Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

Прикарпатський національний університет імені В.Стефаника

Аналітичні розв’язки системи рівнянь гідромеханіки

Система рівнянь гідромеханіки в загальному випадку не має аналітичних розв’язків. Більше того, для загального класу задач для цієї системи не розроблено загальної теорії розв’язності. Тому особливо цінними є такі важливі частинні випадки, що можуть бути вивченими з використанням математичного апарату, а саме класичних методів диференціальних рівнянь. Труднощі, які виникають у тривимірному чисто прикладному випадку, також виникають і багатовимірному випадку. Тому ми не накладаємо ніяких обмежень на вимірність простору. Розглянемо систему рівнянь гідромеханіки в задачах обтікання прямолінійним одновимірним потоком тіла , що в просторі

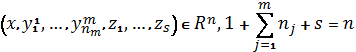
задається співвідношеннями

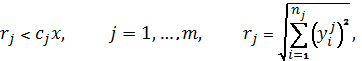
(1)

Для потенціалу швидкості потоку маємо рівняння ([1])

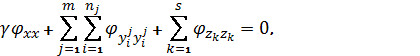(2)

тут дійсне число залежить від числа Маха.

Частинний розв’язок рівняння (2) шукаємо у вигляді де

. (3)

Теорема 1 Автомодельна складова розв’язку рівняння (2) задовольняє рівняння

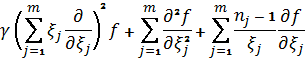= 0 . (4)

Доведення Враховуючи (3), після обчислень послідовно отримуємо

,

,

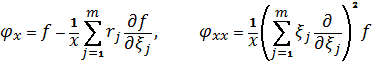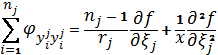і нарешті рівняння (4).

Наслідок 1 При для клина рівняння (4) матиме вигляд

= 0 . (5)

Наслідок 2 При для клиноподібного тіла рівняння (4) матиме вигляд

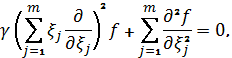(6)

Випадок (відповідає ситуації, коли швидкість потоку близька до швидкості звуку) зводиться до класичного модельного рівняння еліптичного типу.

Наслідок 3 При рівняння (4) матиме вигляд рівняння Лапласа

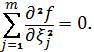(7)

Наслідок 4 При для клиноподібного вістря рівняння (4) матиме вигляд

= 0. (8)

Наслідок 5 При рівняння (4) матиме вигляд

= 0. (9)

Рівняння (5), (8), (9) за допомогою класичних методів інтегруються в квадратурах. Для рівнянь (6), (7) крайові задачі розв’язуться класичними методами. Розв’язання цих та інших частинних випадків рівняння (4) гарно реалізуються в математичних пакетах, наприклад, в Maple.

Зауважимо, що наведені наслідки не охоплюють всіх характерних важливих модельних випадків, і вибрані для ілюстрації методу.

Література:

1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. — Издание 6-е. — М.: Физматлит, 2015. — Т. VI. Гидродинамика. — 728 с. — ISBN 978-5-9221-1625-1.