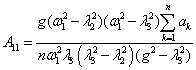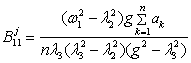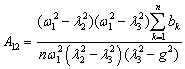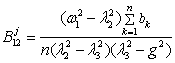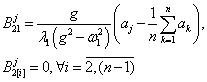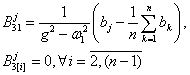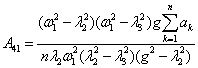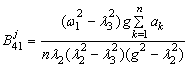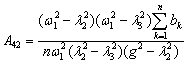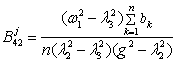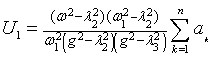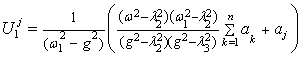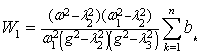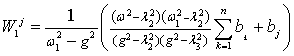Dokukova N.A., Kaftaikina E.N., Konon N.P.

Belarusian State University

INVESTIGATION OF SETS SYNCHRONIZATION OF MOVEMENTS OSCILLATOR WITH ZERO INITIAL CONDITIONS

A dynamical system with a large number n of autonomous oscillators, interacting with one another through a common connection, Figure 1. Each oscillator under external harmonic action of the same frequency and with different initial phases.

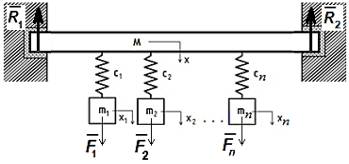
Picture 1 - Vibrations scheme n - oscillators to fixed beam

The equations of motion of the mechanical system shown in Figure 1, the scheme in matrix form becomes:

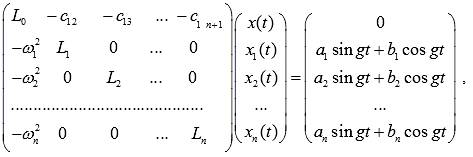
(1)

with following initial conditions:

, , (2)

, _. (3)

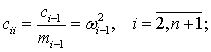
Here , − differential operators of the time parameter t; c_ij – coefficients of elastic elements c_j-1, related to the respective masses m_i-1, ; , ,; , b – the coefficient of viscous resistance of the beam oscillations; – vector of unknown mass movements in the Picture 1; – load vibration acceleration vector mode; , ;
– harmonic forces , are external, attached to an autonomous oscillators - linear force of friction and elastic "Winkler" base in the supports of the beam . The total force - conservative, the strength of the linear friction in the beam, the conservative force of viscous resistance oscillations - .

The characteristic equation takes the form

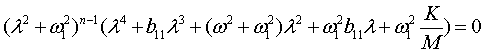, (4)

If the partial frequency n-linear oscillator are the same . Just for simplicity suppose that b = 0. Then the multi-element solutions of the problem leading to the next vibrational modes

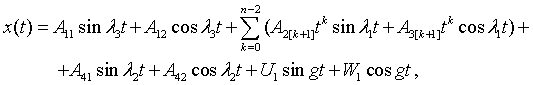(5)

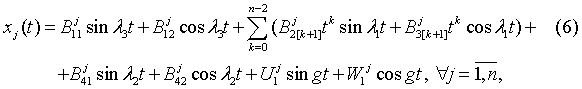
where l₁=w₁, 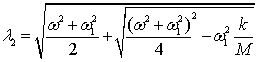,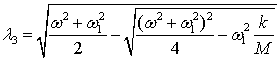. Uncertain factors are relevant decisions by the method developed in [1, 2], analytical formulas for which are summarized in table 1.

Phase difference Δy = y₁ − y₂ is the difference in the initial phase y₁, y₂ two harmonic oscillations of the same frequency y₁= sin(ωt + y₁), y₂=sin(ωt + y₂). With
Δy = 0 fluctuations considered in phase, with Δy = π – antiphase, and with Δy = π/2 or 3π/2 − fluctuations are in quadrature.

Table 1

п/п	beams moving coefficients x(t)	Coefficients movements of autonomous oscillators motion coefficients xj(t),
1	2	3
1
2
3
4
5

We assume that the influence of external forces , annexed to autonomous oscillators are essential have an average frequencies and amplitudes. Consider what might be at the same phase difference y_{j -} y_i between the harmonic oscillator with the same forced frequencies g. The relevant decision can be represented as

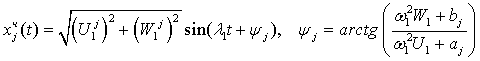_{. (7)}

To make the difference between the phases was π, it is necessary that one of the phases y_j , other y_i. This is possible, when, and any values different signs. Let

_{. (8)}

If , the antiphase occurs when conditions are the same modulo the corresponding coefficients , but always different in sign

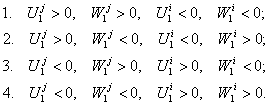(9)

As an example, consider a mechanical system with arbitrary physical parameters : n = 4, M = 25.0 кг, m₁ = m₂ = m₃ = m₄ = 2.1 кг, c₁=c₂=c₃=c₄= 74.0н/м, K=10.0 н/м, a₁=a₂=a₃=a₄=0.0 м, b₁=b₂=b₃=b₄=0.0 м/c, g=3p рад/с, w=3.4986 рад/с,
w₁=5.9362 рад/с, l₁=5.9362 рад/с, l₂=6.8687 рад/с, l₃=0.5466 рад/с, F₁=24.28 н, F₂=19.11 н, F₃=16.25 н, F₄=19.09 н, a₁=1.2 м/с², a₃=4.2 м/с², b₁=11.5 м/с²,
b₃=6.5 м/с². Satisfying one of the conditions antiphase (9), choose option 3 for oscillators with the numbers j = 2 и i = 4. Solving inequalities with respect to the initial conditions a₂, a₄, b₂, b₄ get a₂=7.3177м/с², a₄= -7.328м/с², b₂= -5.41026м/с²,
b₄= 5.376м/с². Their substitution into the formula (5), (6) and Table 1 leads to the following movements:

(10)

a)

b)

c) d)

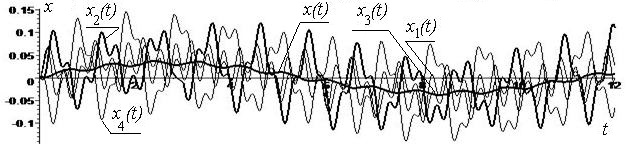
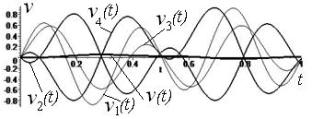
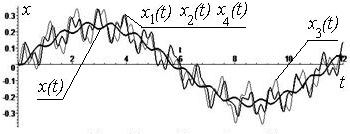
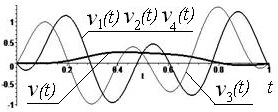
Picture 2 - x(t) and x_j(t) displacements, j = , mechanical system on a, b, c; with v(t), v_j(t) as speed on c. Solutions x₂^ч(t) and x₄^ч(t) are in antiphase on d

Both solutions x₂^ч(t) and x₄^ч(t) They are in opposition for a forced harmonic oscillations with a frequency g=3p рад/с, t can be clearly seen on the graph in Figure 2 c, a, b, d.

In order to have natural oscillations in phase with the zero difference between the phases necessary to satisfy the condition

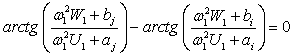_{. (11)}

This is possible if the corresponding coefficients of like harmonics of the external loads F_j и F_i will coincide

(12)

Here condition (12) provides full equivalence of the solutions x_j(t) and x_i(t).

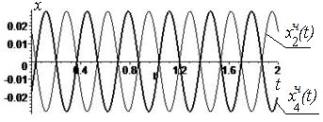
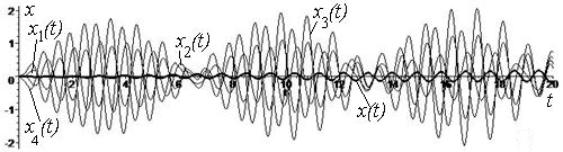
Consider the two-phase synchronization of oscillatory modes of oscillators with the numbers j=1, i=2 and k=4. Select from the following factors when external loads: a₁=a₂=a₄=10.2 м/с², a₃=8.3 м/с², b₁=b₂=b₄= -8.5 м/с², b₃=9.5м/с². There are new solutions, which are in phase of forced oscillations can be observed in motion x₁(t), x₂(t), x₄(t) and figure charts 3.

(13)

In Figures 2 a, b, c, 3 и 4 apparent convergence of the presented solutions according to formulas (5), (6) and tables 1 to the initial conditions (2), (3).

Resonances in the system may have forced displacement, if the frequency of the external load-g coincides with the frequency w₁. We can expect a sharp rise in amplitude at a frequency . The increase will be proportional to the ratio of the number M/K. Choose an arbitrary coefficients of external loads: a₁=4.3 м/с²,
a₂= -5.2 м/с², a₃=9.4 м/с², a₄= -9.2 м/с², b₁= -2.0 м/с², b₂=4.1 м/с², b₃= -0.3м/с²,
b₄= -3.7 м/с² и g= 6.89 рад/с. Increasing the amplitude over time occurs in 2-2,5 figure 4 fold compared b the original and 4. The ratio M/K = 2,5 (1/Гц²).

a) b)

Picture 3 - Displacements x(t) и x_j(t), j = , mechanical system на a, x₁(t), x₂(t) и x₄(t) in phase, with similar conditions . Velocity v(t), v_j(t) on b

a)

b)

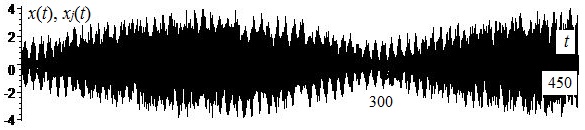
Picture 4 - Displacements x(t) и x_j(t), j = , mechanical system on a, for the period of time from zero to t=450 c on b

References

1. Dokukova N. A. and Konon P. N. General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

2. Dokukova N.A., Kaftaikina E.N. The synchronization of two linear oscillators// Materialy VII miedzynarodowej naukowi-praktycznej konferencji. Przemysl, Polska. 7-15 listopada 2012 r. Przemysl: Nauka i studia, Vol. 18, pp. 28 – 35, 2012.