У математиці вивчення задач на знаходження максимуму й мінімуму почалось давно, тому що більшу частину своїх зусиль людина витрачає на пошук найкращого, тобто оптимального вирішення поставленого завдання. Як, маючи певні ресурси, отримати найвищий життєвий рівень, найвищу продуктивність праці при найменших втратах, максимальному прибутку та мінімальній затраті часу. Так ставляться запитання, над якими доводиться думати кожному члену суспільства. Завдання, метою яких є дати відповідь на дані запитання, отримали назву задачі на екстремуми або задачі на оптимізацію, ї їх роль у житті людей дійсно дуже важлива. Це і обумовлює актуальність даної теми.

Метою роботи є дослідження застосування різних методів розв’язання екстремальних задач відповідно до практичних завдань науки (обчислювальна техніка, фізика, хімія ), а також виробництва та економіки.

Відповідно до мети ставляться такі завдання:

– ознайомитися з такими методами розв`язування задач на екстремум як метод перебору, застосування нерівності Коші, методом диференціального числення;

– розглянути задачу оптимізації, яка розв’язується симплекс-методом та графічно;

– показати практичну значимість задач на екстремум.

Як відомо, загальна задача лінійного програмування полягає в пошуку значень змінних, що задовольняють деяким лінійним обмеженням і забезпечують найбільше (найменше) значення заданої лінійної функції.

Вашій увазі пропоную розв’язати задачу лінійного програмування.

Компанія виробляє полки для ванних кімнат двох розмірів – А и В. Агенти з продажу вважають, що за тиждень на ринку може бути реалізовано до 550 полок. Для кожної полки типу А треба 2 м² матеріалу, а для полки типа В – 3 м² матеріалу. Компанія може отримувати до 1200 м² матеріалу на тиждень. Для виготовлення однієї полки типу А треба 12 хв машинного часу, а для виготовлення однієї полки типу В – 30 хв; машину можна використовувати 160 год на тиждень. Якщо прибуток від продажу полок типу А складає 3 грошові одиниці, а від полок типу В – 4 грошові одиниці, то скільки полок кожного типу слід випускати за тиждень?

Складемо математичну модель задачі. Нехай – кількість полок виду А,

– кількість полок виду В, які виробляються за тиждень (за умовою задачі ці змінні невід´ємні). Прибуток від продажу такої кількості полок складе , прибуток треба максимізувати. Випишемо обмеження задачі.

– за тиждень на ринку може бути реалізовано до 550 полок.

Витрати матеріалу:

Витрати машинного часу:

Таким чином, приходимо до задачі лінійного програмування.

Розв´яжемо задачу симплекс-методом.

Уведемо три додаткові змінні

Маємо задачу:

Виберемо наступний опорний план =(0, 0, 550, 1200, 9600).

Складемо симплекс-таблицю.

Таблиця 2.3.1.

Базис	План
	550	1	1	1	0	0
	1200	2	3	0	1	0
	9600	12	30	0	0	1
	0	–3	–4	0	0	0

В останньому оціночному рядку є від´ємні оцінки, тому треба робити крок симплекс-методу. Вибираємо стовпець с найменшою оцінкою, а потім розрішаючий елемент – за найменшим відношенням вільних членів до коефіціентів стовпця (останній стовпець). Результат кроку запишемо в таблицю (розрішаючий елемент будемо виділяти жирним шрифтом).

Аналогічно будемо повторювати кроки, поки не прийдемо до таблиці з невід´ємними оцінками.

Таблиця 2.3.2

Базис	План
	230		0	1	0
	240		0	0	1
	320		1	0	0
	1280		0	0	0

Таблиця 1.3.3.

Базис	План
	50	0	0		0
	300	1	0		1
	200	0	1		0
	1700	0	0		0

Таблиця 2.3.4.

Базис	План
	1200	0	0	24	–18	1
	450	1	0	3	–1	0
	100	0	1	–2	1	0
	1750	0	0	1	1	0

Оскільки в останньому плані рядок не містить від´ємних значень, то план є оптимальним, цільова функція приймає значення 1750.

Таким чином, щоб отримати максимальний прибуток, підприємству необхідно

виробляти 450 полок виду А та 100 полок виду В, при цьому прибуток складе 1750 грошових одиниць, та залишиться невикористаними 1200 хвилин (20 годин) машинного часу.

Розв´яжемо задачу графічним методом. Побудуємо область допустимих розв’язків. Побудуємо прямі й визначимо, яку півплощин
у визначає дана нерівність. Пряму будуємо з урахуванням умови та (для побудови покладемо , ). При умові що , будуємо:

. Нерівність визнає півплощину під прямою.

. Нерівність визначає півплощину, розташовану під прямою.

. Нерівність визначає півплощину, розташовану під прямою.

Знайдемо точки перетину прямих і змінимо параметри прямих, залишивши область обмежень.

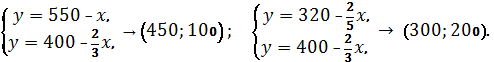
Враховуючи, що , (нерівності визначають першу координатну четверть), шукана область визначена многокутником.

Побудуємо тепер нормальний вектор цільової функції . Цей напрямок вказує на напрямок зростання цільової функції . Пряма, задана рівнянням , представляє собою “нульову” лінію рівня функції . Ця пряма проходить через початок координат і перпендикулярна вектору . Рухаючи цю пряму паралельно саму до себе, фіксуємо її крайнє положення, яке проходить через точку .
.

При числі параметрів, які оптимізуються, понад три отримувати графічне рішення неможливо. Для таких випадків розроблені різні ітераційні прийоми розрахунку, які реалізуються на ЕОМ.

Використання екстремальних задач виправдано тим, що вони з достатньою повнотою закладають розуміння того, як людина шукає, постійно вирішує життєві задачі так, щоб отримані результати її діяльності були якнайкращі. Розв'язуючи екстремальні задачі, бачимо велику ефективність їх застосування до розв’язання життєво практичних задач.

Застосування диференціального числення допомагає усвідомити, що функція, задана аналітичною формулою, може виражати залежності між реальними величинами в найрізноманітніших явищах і процесах. Похідна знаходить широке застосування у фізиці та є найважливішим інструментом економічного аналізу.

Питання оптимізації ми зустрічаємо у будь-якій сфері людської діяльності.

Таким чином, розв’язання екстремальних задач допомагає поглибленню і збагаченню математичних знань. Ці задачі суттєво впливають на аспекти застосування вивченої теорії на практиці.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Практическая оптимизация / Гилл Ф., Мюррей У., Райт М. - М.: Мир, 1985.-509 с.

2. Методы решения экстремальных задач и их применение в системах оптимизации / Евтушенко Ю.Г. - М.: Наука, 1982. - 432 с.

3. Прикладная математика / Усольцев Л.А. - Омск: Изд-во СибАДИ, 2008. - 68 с.

4. Алгебра [підручник для класів з поглибленим вивченням математики]/ А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір. - Х.: Гімназія, 2011. - 144, [1] с.