Сатыбалдиев О.С., Мендебаев Ж.Б.

Қ.И.Сәтбаев атындағы ҚазҰЗТУ, Қазақстан Республикасы

Еркін сауда моделі

Физика мен химия, биология мен психология, социология мен архитектура ғылымдарының нақты және айқын қолдану аймақтары бар. Лазер сәулесі мен ацетилен синтезі, клетканың құрамы мен жеке меншік қағидасы, топырақтың эрозиясы мен Рим империясының құлауы нақты және көрнекті объектілермен, заттармен немесе белгілі заңдылықтармен тығыз байланысты. Оларды зерттей аламыз, себебі олар біздің сезім органдарымыз қабылдайтын қоршаған орталардан тұрады. Математикада, керісінше, сан, функция, жиын, операция және т.б. секілді табиғатта жоқ, адам баласының ойлау қабілетінің жемісі болып табылатын абстрактылық түсініктер қарастырылады.

Әрбір ғылымның басқа ғылымдардан айқын бөліп тұратын өзіндік шекарасы бар. Мысалы, физик жекеменшіктің әртүрлі формаларының арасындағы қатынастарды зерттеуге қауқарсыз. Тарихшы химиялық реакциялардың заңдылықтарын зерттей алмайды. Ботаник өзінің кәсіби бағдарларын Рим империясының заңдылықтарын талдауға қолдана алмайды. Ал математик ғылымдардың арасында туындаған осындай жасанды шекараларға жол бермейді және алдында кездескен кезкелген кедергілерден тайсалмай өте алады. Таза математик бола тұра, ол адамзат іс-әрекетінің кезкелген формасына еркін ене алады және оларды зерттеуде айтарлықтай табысқа жете алады.

Мынандай сауалдың туындайтыны заңды құбылыс. Нақты қолданбалы мәселелерді шешудегі абстрактылы математикалық әдістердің керемет жетістіктерін қалай түсіндіруге болады? Бізді қоршаған ортада жоқ сан мен функция, теңдеулер мен операторлар неге планеталар қозғалысының, химиялық элементтердің өзара әсерлерінің, генетикалық ақпараттардың берілулерінің, еркін нарықтағы баға механизмдерінің құпиясын ашуға мүмкіндік береді? Басқаша айтқанда, абстрактылы дүние нақты көрнекті дүниеге неге айналады? Бұл айтылған мәселелерге толық жауап бар. Математика мен бізді қоршаған нақты дүниені міндетті түрде байланыстыратына бір ғажайып нәрсе бар. Ол нақты ғылымдардың айқындаған заңдылықтарын қатаң математикалық тілге айналдыратын зерттеліп отырған құбылыстың математикалық модельдері болып табылады.

Математикалық моделдеу бір-біріне сорпасы қосылмайтын екі дүниені, яғни біздің органдарымыздағы сезім мүшелері қабылдайтын және қоршаған жеке ғылымдардың көмегімен зерттелетін бізді қоршаған шындық дүние мен математиканың заңдары үстемдік ететін абстрактылы дүниені қосатын алып көпір болып табылады.

Еркін саудадағы тауарлар бағасы мен халық табысының өзгеру механизмін қарастыралық. Бір-бірімен бәсекелес және тәуелсіз тауар өндірушілер мен сатушылардың саны өте көп болсын деп ұйғаралық. Қарапайымдылық үшін шығарылатын өнім көлемі өзгермейді деп есептелік. Халық табысының өзгеру жылдамдығы оның табысы -ге тура пропорционал болсын. Халықта қаражат неғұрлым көп болған сайын, соғұрлым үлкен өзгерістер болады. Тұрғындар тұрақты табыс көзіне ие және қолда бар ақша қаражаты тек қана сол көрсетілген тауарларды алуға жұмсалады деп есептелік. Тұтынатын тауарлар болмаған жағдайда ешқандай қаржы жұмсалмайтыны айтпаса да түсінікті, демек, халық табысы тұрақты жылдамдықпен өседі. Кіріс пропорционал коэффициенті болатын, баға деңгейіне пропорционал тауарларды алу есебінен төмендейді. Сөйтіп, халық табысының жылдамдығы

теңдігімен анықталады екен.

Бағаның өзгеру жылдамдығы баға деңгейіне пропорционал, сонымен қатар халық табысы болмаған жағдайда тауар алынған соң амал жоқтықтан жылдамдығына кемітеді. Баға өсуі пропорционалдық коэффициенті болатын халық табысының өсу мөлшері бойынша жүзеге асырылады. Нәтижесінде бағаның өзгеру жылдамдығы үшін

формуласын аламыз.

Осы ұйғарымдар бойынша халық табысы мен тауар бағасының өзгерісі төмендегі дифференциалдық теңдеулер жүйесі арқылы айқындалады

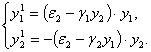(1)

Бұл есептің шешімі уақыт бойынша периодты түрде өзгеріп отырады.

Бастапқы уақыттағы халықтың табысы және баға деңгейі төмен болсын деген ұйғарым жасалық, яғни теңсіздіктері орындалсын. Бұл жағдайда -дің туындысы оң, ал -нің туындысы теріс болады, халықтың кірісі төмен болғанда, оның сатып алу мүмкіншілігі де аз болады. Бұл деп атырғанымыз шығарылған тауарлардың барлығы сатылмайды деген сөз (бұл модельде шығарылған өнім көлемі өзгермейтінін еске түсірелік). Жұмысын тоқтату немесе жабылып қалу қауіпі әрқашан туындап тұратын еркін сауда бәсекелестік жағдайында өндіріс қожайыны қалай ма, қаламай ма тауар бағасын төмендетуге мәжбүр. Зерттеу процесінің бірінші кезеңінде осының салдары болатын тауар бағасының төмендеуі мен халық табысының өсуін байқаймыз. Ерте ме, кеш пе халық табысы өте жоғары болатын және теңдігі орындалатын уақыт мезгілі туындайды. Бұл жағдайда (1) жүйенің екінші теңдеуінің оң жағы нөлге тең болады. Бұл функциясының экстремумына (бұл жағдайда минимумына) сәйкес келеді. Баға деңгейінің төмен болғандықтан, халық табысы өсе бастайды. Сөйтіп,

қатынастары орындалады.

Зерттеу процесінің екінші кезеңінде халық табысы өте жоғары, ал баға деңгейі өте төмен болады. Бұл жағдайларда (1) жүйенің теңдеулеріне сәйкес екі туынды да оң болады, яғни, біз әрі халық табысының өсуін (баға әліде төмен), әрі бағаның өсуін (халықтың сатып алу мүмкіндіктері әліде жоғары) байқаймыз. Өсетін функциясының қатынасын (мәнін) қабылдайтын уақыт мезгілі туады. Осыдан кейін

қатынастары орындалады. Сөйтіп, біз, халық табысының төмендеуін (баға өте жоғары) және бағаның өсуін (халықтың сатып алу мүмкіншілігі жоғары) сипаттайтын зерттеу процесінің үшінші кезеңіне келеміз. Халық табысының төмендеуіне сәйкес теңдігі орындалатын уақыт мезгілі туады. Осыдан соң

шарттары орындалып, халық табысының төмендеуі (баға әлі де болса жоғары) және халықтың сатып алу мүмкіншіліктеріне сәйкес бағаның құлдырауы байқалады. Бұл процесс баға шамасына дейін төмендейтін уақыт мезгіліне дейін жалғасады. Осыдан кейін бағаның төмендеуі және халықтың сатып алу мүмкіншіліктерінің төмен болуына сәйкес алдағы уақытта баға деңгейін төмендетілуі есебінен халық табысының өсуін сипаттайтын бірінші кезеңге қайта ораламыз. Сөйтіп, қарастырылып отырған процесс үшін жаңа цикл басталады.

Осы алынған нәтижелер экономикалық заңдылықтар физикалық, химиялық және т.б. заңдылықтар сияқты шындық дүниені бейнелейтіндіктерін көрсетеді.

Еркін саудада өнеркәсіп иесі халықтың сатып алу мүмкіншіліктерінің төмендеуіне қарай бағаны төмендете алмайды, себебі, оның бәсекелестіктері қуып жетеді де, өз тауарларын тез арада сатып үлгіреді. Күшті бәсекелестік жағдайында төменгі бағада болса да тауарларды тезірек өндіруге тырысу қажет. Екінші жағынан, халық табысы өте жоғары болған сайын, сатылымдағы тауарларды тез сатып алады. Бұл модельде айтылған сұраныс пен ұсыныстың арасындағы баланста қолдау мәселесі бағаны өсіру арқылы жүзеге асырылады.

Осы жоғарыда айтылғандарға сәйкес жүргізілген компьютерлік эксперименттің нәтижесі төмендегідей. Біз, ең алдымен, уақытқа қарай зерттелініп отырған процесстің периодтық түрде өзгеретіндігіне көз жеткіздік. Бастапқыда берілген шарттарды өзгерте отырып, сұраныс пен ұсыныстың бір-біріне сәйкестігінде тепе-теңдік қалпы орындалатынды.

Әдебиет

1. Каданер Э.Д. Динамическое моделирование экономических систем. Пермь, 2012, -279c.
2. Пугачев В.Ф., Пителин А.К. Анализ вариантов антиинфляционной экономической политики экономике // Экономика и математические методы, 2013, №3. - C.31-42.

3. Яглом И.М. Математические структуры и математическое моделирование. – М., Наука, 2007. - 247c.

4. Пененко В.В., Алоян А.Е. Модели и методы для задач окружающей среды. – Новосибирск: Наука, 2011. - 159c.