Математика/ 4. Прикладна математика

К.ф.-м.н.  Казмерчук А.І.,

Бедрій В. М.

Прикарпатський національний університет імені В.Стефаника

Оптимальні сіті сортування з одним ненадійним компаратором

Ми вивчаємо клас методів сортування, що задовольняє обмеження у тому сенсі, що послідовність порівняння елементів набору дійсних чисел не залежить від результатів попередніх порівнянь. А саме, якщо ми порівнюємо елементи і , то наступні порівняння у випадку мають бути таким ж, що і у випадку .

Нехай – мінімальна кількість порівнянь, якої достатньо для сортування елементів. Для малих значень точні значення або оцінки для них наведені в [1]. В роботі [2] знайдено точне значенні і .

В даній роботі ми розглядаємо не цілком надійні сіті сортування в тому сенсі, що, можливо, якийсь один з компараторів не впорядковує пару вибраних елементів, а залишає їх на своїх місцях. Нехай – мінімальна кількість порівнянь в сіті сортування з одним ненадійним компаратором, якої достатньо для сортування елементів. Встановлено загальні двосторонні оцінки і знайдено точні значення для всіх натуральних .

Далі ми використовуємо наступне твердження.

Теорема 1 Сіть сортує в порядку зростання всі послідовності з та тоді і тільки тоді, коли вона сортує будь-який набір з дійсних чисел.

Цей результат випливає з принципу нулів та одиниць [1], який, в свою чергу, є частинним випадком теореми Бурисіуса.

Теорема 2 Для кожного натурального справджується оцінка

(1)

Доведення Оскільки один з компараторів не впорядковує вибрану пару, то, очевидно, мінімальна кількість компараторів в сіті не менше, ніж на 1 більша від Далі, якщо в оптимальній сіті з надійними компараторами продублювати кожний компаратор, то така сіть сортуватиме будь-який набір з дійсних чисел.

Справджується і більш загальне твердження.

Теорема 3 У випадку сіті сортування з ненадійним компараторами при кожному натуральному для оптимального значення справджується оцінка

. (2)

Доведення Оскільки компараторів не впорядковують вибрані пари, то, очевидно, мінімальна кількість компараторів в сіті не менше, ніж на більша від Далі, якщо в оптимальній сіті з надійними компараторами кожний компаратор взяти раз, то така сіть сортуватиме будь-який набір з дійсних чисел.

Теорема 4 Для кожного натурального справджується оцінка

(3)

Доведення Оцінка (3) є прямим наслідком оцінки ([2]) .

Нехай . Тоді, очевидно, набір вже впорядковано і тому .

Нехай . Тоді перший компаратор може виявитися ненадійним, а двох порівнянь зрозуміло, цілком вистачає. Отже, . Це випливає також і з оцінки (1), бо, як відомо,

Нехай . Оскільки ([1]) , то з оцінки (1) випливає, що . Програмно було знайдено, що .

Наприклад, сіть 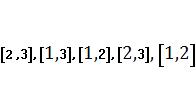, зображена на рис. 1, сортує будь-який набір трьох дійсних чисел. У цьому можна переконатися з використанням Теореми 1, можливо, за допомогою обчислювальних засобів.

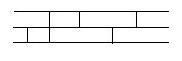
Рисунок 1

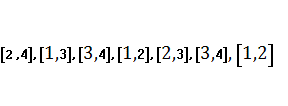Нехай . Оскільки ([1]) , то з оцінки (1) випливає, що . А з оцінки (3) випливає, що . Було знайдено сіть , яка зображена на рис. 2, що сортує будь-який набір чотирьох дійсних чисел.

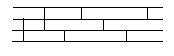
Рисунок 2

Нехай . Оскільки ([1]) , то з оцінки (1) випливає, що . З оцінки (3) також випливає, що . Було знайдено сіть

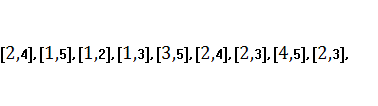
, яка зображена на рис. 3, що сортує будь-який набір п’ятьох дійсних чисел.

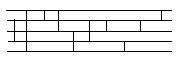
Рисунок 3

Теорема 5 .

Література:

1. Дональд Кнут. Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е изд. — М.: «Вильямс», 2007. — 824 с. — ISBN 5-8459-0082-4.

2. Michael Codish, Luis Cruz-Filipe,Michael Frank, Peter Schneider-Kamp ,-

Twenty-Five Comparators Is Optimal When Sorting Nine Inputs ,- (ICTAI)

(2014),- pp: 186-193,ISBN: 978-1-4799-6572-4