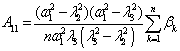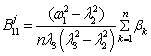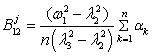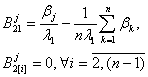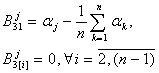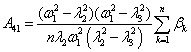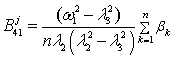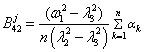Dokukova N.A., Kaftaikina E.N.
The Belarusian State University
Natural oscillations synchronization of multi-element-dynamical system of autonomous oscillators

The dynamical system of n autonomous oscillators is considered (Figure 1), each of oscillators is secured to the beam having a resilient termination. Oscillators receive the deviation and possess the speed at the initial time. It is necessary to determine the values of these kinematic parameters to provide phase, antiphase and other types of objects synchronizations which are interacting with each other through a common connection.

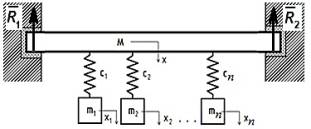
Figure 1 - Oscillation scheme of n oscillators secured to the beam

The system of motion equations of the mechanical system is provided in matrix form: (1)

with initial conditions , , (2)

, _. (3)

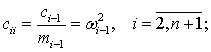
Here , − differential operators with parameter of time t; c_ij – coefficients of elastic elements c_j-1, assigned to the corresponded masses m_i-1, ; , ,; , b – the coefficient of viscous resistance of the beam oscillations; – vector of unknown mass displacements in Figure 1; and – linear force of friction and elastic "Winkler" base in the supports of the beam . Common force - conservative, the strength of the linear friction in the beam, nonconservative force of viscous resistance oscillations - .

The characteristic equation takes the form:

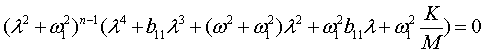, (4)

if the partial frequencies of all n-linear oscillators are identical . For simplicity, set b = 0. Then the multi-element solutions of the problem leading to the next vibrational modes

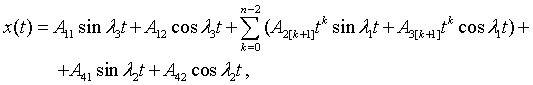(5)

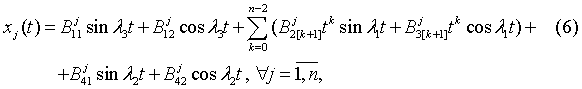
where l₁=w₁, ,.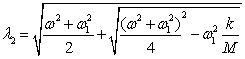

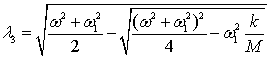Uncertain coefficients of relevant decisions are defined using the method developed in [1, 2], which analytical formulas are shown in Table 1.
If we put n= 2, с₁₂=с₁₃, a₁=a₂=b₁=b₂=b=K= 0 and choose the following conditions as initiala₁ =g, a₂ =d, b₁=b₂ = 0, then obtained analytical formulas of solutions, fully coincide with displacements in [2].

If n=N (N), , b_i = 0 (), b= 0, K= 0, then the obtained analytical formulas solutions are fully coincided with displacements in [3, 4] taking into account the absence of a load mode.

As an example, consider the mechanism with arbitrary physical parameters: n=5, M=20kg, m₁=m₂=m₃=m₄=2kg, c₁=c₂=c₃=c₄=485kg/s², K=125.0 kg/s², a₁=-10сm, a₂=6сm, a₃=-2сm, a₄=4сm, a₅=-5сm, b₁=60сm/s, b₂= -90сm/s, b₃=40сm/s, b₄= -70cm/s, b₅=80cm/s, w=11.292 rad/s, w₁=15.572 rad/s, l₁=15.572 rad/s, l₂=19.127 rad/s, l₃=2.035 rad/s.

Table 1

№	Beam displacements coefficients x(t)	Coefficients of autonomous oscillators displacements xj(t),
1	2	3
1
2
3
4

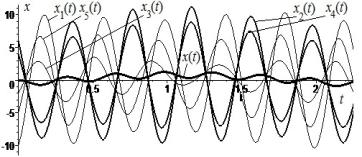
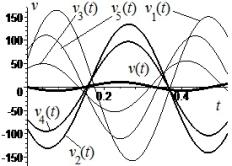
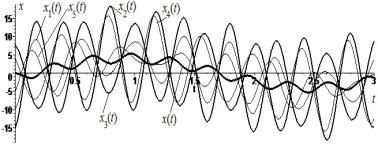
Displacement and velocity of components are plotted in Figure 2 and on the basis of formulas (5) and (6), Table 1 will take the form:

a) b)

Figure 2 - Displacements x(t) and x_j(t) , j = of dynamical system consisting of 5 identical oscillators on an elastic beam with different initial conditions on a and velocity v(t), v_j(t) on b

If the difference between squares of the frequencies is a great value in comparison to other differences, that vibrations with the natural frequency l₁ will have the greatest amplitudes. Consider what phase differences jj - ji could be between the harmonic oscillator with the same natural frequencies l₁. The corresponding particular solution can be represented as:

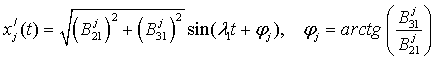_{. (8)}

It is necessary that one of the phases j_j , other j_i to get the difference π between phases of two oscillatory processes and . It’s possible, for example, when and any numbers with different signs. Lets

_{. (9)}

If , then antiphase occurs when the correspondent coefficient are the same module , but always are different sign.

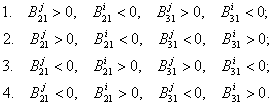(10)

Lets change the characteristics of the initial conditions for the provided example in order to the displacement of the second oscillator is in antiphase to the third one using case 2. Lets define what should be a₂, b₂, a₃, b₃ on the basis of inequalities (10) and the coefficients of the table 1. This results in the following relationships between the parameters:

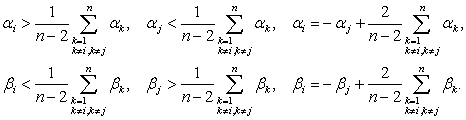(11)

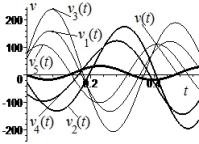
Lets a₃= -15.0 cm and b₃=75.0 cm/s, then a₂=7.67 m, b₂= -28.33 cm/s, in i=2, j=3, n=5. Their substitution into the formula (5), (6) leads to other displacements:

Two solutions x₂(t) and x₃(t) are in antiphase of harmonic oscillations with the natural frequency l₁ = 15.6 rad/s, which can be clearly seen in the overall displacements graphs in Figure 3.

In order to the natural oscillations are in phase with zero difference between the phases, it is necessary to satisfy the condition:

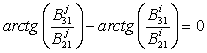_{. (13)}

It’s possible if

_{. (14)}

The algebraic expression (14) is trivial in the case when the corresponding initial conditions (2) and (3) at least in two oscillators under consideration coincide a_j = a_i and b_j = b_i.

a b

Figure 3 - Displacements x(t) and x_j(t), j = of the dynamical system on а, x₂(t) and x₃(t) are in antiphase on frequency l₁, velocity v(t), v_j(t) on b

Figures 2 and 3 are presented the convergence of the solutions according to the formulas (5), (6) and Table 1 to the initial conditions (2) and (3).

References:

1. Dokukova N. A. and Konon P. N. General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

2. Dokukova N.A., Kaftaikina E.N. The synchronization of two linear oscillators// Materialy VII miedzynarodowej naukowi-praktycznej konferencji. Przemysl, Polska. 7-15 listopada 2012 r. Przemysl: Nauka i studia, Vol. 18, pp. 28 – 35, 2012.

3. Dokukova N.A., Kaftaikina E.N., Konon P. N. About synchronous oscillations of multi-linear dynamical systems // Materials of the X International scientific and practical conference, «Conduct of modern science», November 30 - December 7, 2014.- Mathematics. Physics. Modern information technologies. - V. 21. - Sheffield. Science and education Ltd. Registered in england & wales. Registered Number: 08878342. Sheffield, S Yorkshire, England, - 2014. - С. 25-32.

4. Dokukova N.A., Katakana E.N., Konon P.N. Synchronous oscillations of n-autonomous oscillator on a single inelastic fixed-ended beam // X International scientific practical conference "Bdescheto Ask a question from light to Naukat - 2014". Mathematics. Physics. Svremenni on information technology "Byal GRAD-BG" Ltd., c. Sofia. Republica Bulgaria. - 2014. - T. 18. - S. 19-25.