Технические науки/4. Транспорт

Тогизбаева Б.Б., Бекжан Ж.О., Тогизбаев Б.К., Алинова А.С.

Евразийский национальный университет им.Л.Н.Гумилева, Казахстан

Исследование напряженно-деформированного состояния сыпучего груза

Анализ напряженно-деформированного состояния рудной массы в подвижном составе производится с использованием программного комплекса ANSYS. При этом необходимо решить следующие задачи:

– разработка модели объекта исследования;

– построение конечно-элементной сетки;

– расчет напряженно-деформированного состояния рудной массы;

– определение функциональной зависимости напряжений s_x^max, s_y^max, s_xy^max, перемещений u_x и u_y от значения модуля Юнга;

– обработка полученных результатов;

– обобщение данных и выводы.

В качестве объекта исследования предложено:

- рудная масса в бункере с щелевым выпускным отверстием;

Модель нагружается распределенной нагрузкой q=45 МПа в вертикальной плоскости.

Для анализа зависимости напряжения и перемещения от модуля упругости необходимо провести несколько экспериментов с разными значениями модуля упругости Е₆.

База конечных элементов ANSYS содержит более 100 видов конечных элементов, каждый из которых определяет применимость элемента к той или иной области расчетов (прочностной, тепловой анализы, движение жидкости и т.п.), характерную форму элемента (линейную, плоскую, в виде бруска и т.д.), а также двумерность или трехмерность элемента как геометрического тела. Для поставленных задач был выбран элемент SOLID92.

SOLID92— это усложненная версия двумерного, трехузлового элемента. Усовершенствование элемента обеспечивает более точные результаты исследований со смешанной автоматической сеткой. Также данный конечный элемент поддерживает неправильные формы без искажений точности [1].

Исследование напряженно-деформированного состояния рудной массы проводилось методом конечных элементов в программном комплексе ANSYS. При построении имитационной модели системы «бункер-рудная масса» был использован конечный элемент тетраэдр solid92.

При выполнении условия непрерывности перемещений с математической точки зрения метод конечных элементов эквивалентен методу Ритца. Расчет по МКЭ проводится в следующей последовательности:

1. Разбиение сплошной среды тела на конечные элементы и назначение узлов, в которых определяются перемещения.

2. Выбор зависимости перемещения внутри каждого элемента через перемещения узлов. С помощью этой зависимости определяются деформации и напряжения через узловые перемещения.

3. Построение матрицы жесткости элементов и составление системы линейных алгебраических уравнений равновесия.

4. Решение системы алгебраических уравнений.

5. Определение компонентов напряженно-деформированного состояния тела.

Количество конечных элементов 8870. Граничные условия: грани расчетной модели жестко закреплены, т.е. перемещение по осям координат равны нулю. Максимальные напряжения возникают в нижней части образующегося купола. Максимальные напряжения на рисунках обозначены – МХ, минимальные-MN. Значения напряжений приведены в правой части рисунка

Поскольку рудная масса сопротивляется разрушению при растяжении значительно слабее, чем при сжатии, то очевидно, что разрушение свода будет формироваться и распространяться в зоне растягивающих напряжений.

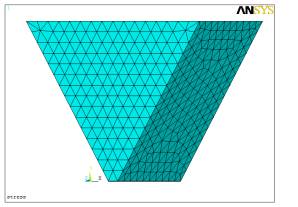
Рисунок 1 – Конечно-элементная модель бункера

Для моделирования условий контакта, задавались коэффициенты трения между рудной массой и стенкой бункера.

Анализ результатов моделирования позволил изучить закономерности изменения напряженно-деформированного состояния рудной массы, что затруднительно получить при аналитическом исследовании, а также позволил установить зоны образования сводов [2].

Используя прямоугольную систему координат и обозначая координаты точки через (x, y, z) смещения через (u, v, w), деформации через ε_х, ε_у, ε_z, γ_xy, γ_xz, γ_yz, а напряжения через, можно записать соотношения между смещениями и деформациями в виде

(1)

,

Рассмотрим задачу о распределении деформаций и напряжений в изотропном трехмерном упругом теле, как рудная масса под воздействием статистической нагрузки.

Связь между напряжениями и деформациями можно выразить следующим образом

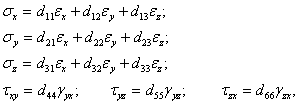(2)

где Е и ν соответственно модуль продольной упругости и коэффициент Пуассона.

Предполагая, что внутри отдельных элементов напряжения (а, следовательно, и деформации) постоянны, для смещений внутри элемента можно пользоваться приближенными уравнениями первого порядка

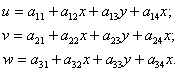(3)

Обычно в качестве дополнительного общего выражения используется принцип минимума потенциальной энергии заключенный, например, в бункерах. Можно использовать и условия равновесия сил, по проще применять принцип минимума потенциальной энергии.

Принцип наименьшей потенциальной энергии утверждает, что «среди всевозможных u, v, w истинными являются те u, v, w при которых значение П минимально». Это равносильно (в используемой терминологии) уравнениям равновесия сил.

Исследования закономерности изменения напряженно-деформированного состояния рудной массы позволили аналитически определить области образования свода в бункере и расчетные схемы для определения максимального сводообразующего размера спуска бункера при cовместной работе с ленточным питателем и определения угла наклона передней и задней стенок спуска бункера.

Литература:

1.Тутанов С.К. Управление состоянием массива горных пород . Караганда: КарГТУ, 2004.-107с.

2. Тогизбаева Б.Б. Выбор основных параметров истечения рудной массы из бункеров.-Караганда, изд.Санат, 2010.-127 с .