Математика/ 1. Диференціальні і інтегральні рівняння

К.ф.-м.н.  Казмерчук А.І.

ДВНЗ “Прикарпатський національний університет імені Василя Стефаника”

В’язкісно-згладжувальний метод розв’язання задачі Коші для квазілінійного рівняння з частинними похідними першого порядку

У роботі вивчаємо новий метод розв’язування задачі Коші для квазілінійного диференціального рівняння з частинними похідними першого порядку            

(1)

(2)

де .

Означення 1 Обмежена вимірна функція називається узагальненим розв’язком задачі (1),(2), якщо

виконується нерівність

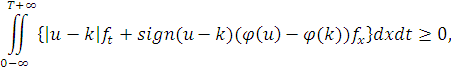
а початкова умова (2) приймається у сильному сенсі.

Загальна теорія розв’яності задачі (1),(2) була побудована в 50-70-х роках минулого століття в роботах Олійник О. А., Кружкова С. М., Lax P. Викликає інтерес питання отримання розв’язків за допомогою конструктивних методів побудови наближених розв’язків. В роботах [1],[2] Казмерчука А. І. було розглянуто як конкретні методи, так і загальний підхід, який дозволяє обґрунтовувати збіжність разом з отриманням оцінок швидкості в наближених методах. В даній роботі ми розглядаємо апроксимації задачі (1), (2), які будуються на основі одночасного застосування методу в’язкості і методу згладжування.

Нехай і при , – розв’язок задачі Коші

(3)

(4)

зі згладженою початковою функцією за допомогою середніх функцій.

Далі, нехай при , – класичний розв’язок задачі Коші

(5)

(6)

В цій роботі отримано оцінки збіжності наближених розв’язків до узагальненого розв’язку задачі (1),(2) у наступному сенсі.

Означення 2 При функція , яка на різних смугах є почерговим розв’язком задачі (3),(4) і задачі (5),(6) , називається наближеним розв’язком задачі (1),(2), отриманим з допомогою в’язкісно-згладжуваного методу

Теорема 1 Нехай  . Тоді для наближеного розв’язку , отриманого з допомогою в’язкісно-згладжуваного методу, виконується оцінка

де функція залежить від модуля неперервності в початкової функції .

Теорема 2 Нехай . Тоді для наближеного розв’язку , отриманого з допомогою в’язкісно-згладжуваного методу, виконується оцінка

Теорема 3 Нехай  . Тоді для наближених розв’язків та , отриманих з допомогою в’язкісно-згладжуваного методу, і таких, що відповідають початковим функціям та виконується оцінка

де функція залежить від сумісного модуля неперервності в початкових функції та .

Теорема 4 Нехай і Тоді для наближених розв’язків та , отриманих з допомогою в’язкісно-згладжуваного методу, і таких, що відповідають початковим функціям та виконується оцінка

Доведення теорем аналогічне до доведення тверджень в [2] і ґрунтується на оцінці функціонала

із застосуванням оцінок для модулів неперервності в наближених розв’язків, які дозволять отримати компактність сім’ї наближених розв’язків.

Зауважимо, що варіація ширин смуг, на яких почергово застосовуються метод в’язкості та метод згладжування дозволяє оптимізувати швидкість збіжності наближених розв’язків до точного.

Із теорем 1-4 незалежно можна отримати існування узагальненого розв’язку задачі (1),(2).

Література:

1.Казмерчук А. И. О сходимости приближённых решений задачи для квазилинейных уравнений первого порядка. - Вестник МГУ. - Сер. матем. механ.,-1989.-Вып.4,с.68-70

2.Казмерчук А.І. До обґрунтування наближених методів розв’язання квазілінійних законів збереження з негладкими даними задачі. - Вісник національного університету “Львівська політехніка”, Прикладна математика.-2000.-№411.-с.147-151