Математика 3. Теория вероятностей и математическая статистика

К.ф.-м.н. Симогин А.А.

Донбасская национальная академия строительства и архитектуры,
г. Макеевка

Стоимость барьерного опциона продажи в модели Мертона

Одной из основных задач финансовой инженерии является определение справедливой стоимости производных финансовых инструментов. В настоящее время на финансовом рынке производных финансовых инструментов наряду со стандартными опционами все большую популярность приобретают экзотические опционы [1]. Ярким представителем класса экзотических опционов является барьерный опцион. Свою заслуженную популярность барьерные опционы различных видов приобрели из-за их более низкой стоимости по сравнению со стандартными. В данной работе рассмотрена задача нахождения стоимости двухбарьерного опциона продажи европейского типа, в случае если эволюция стоимости базового актива имеет скачкообразную траекторию.

Пусть – пуассоновский процесс с постоянной интенсивностью , который порождает возрастающую непрерывную справа фильтрацию .

Рассмотрим на полном вероятностном пространстве финансовый –рынок с непрерывным временем. Будем предполагать, что размер банковского счета описывается детерминированной функцией, которая удовлетворяет дифференциальному уравнению

, , (1)

где – процентная ставка.

Эволюция изменения стоимости базового актива удовлетворяет стохастическому дифференциальному уравнению

, (2)

где , .

Согласно лемме Ито для процесса со скачками, решение уравнения (2) можно записать в виде

.

Данный рынок является [2] полным безарбитражным. Плотность единственной мартингальной меры относительно исходной меры имеет вид

,

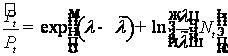где – интенсивность пуассоновского процесса относительно мартингальной меры .

Введем в рассмотрение на данном финансовом –рынке опцион продажи европейского типа с платежной функцией

, (3)

где – цена базового инструмента в момент погашения опциона, – страйк, и соответственно нижний и верхний барьеры, причем .

Теорема.

В модели финансового –рынка (2)–(3) стоимость двухбарьерного опциона продажи с платежной функцией вида (3) можно представить в виде

,

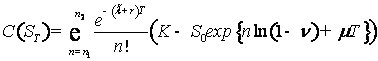где

, .

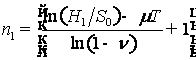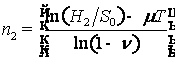Доказательство. Согласно общей теории финансовый обязательств [2, 3] стоимость европейского опциона с платежной функцией определяется соотношением

,

– усреднение по мартингальной мере

Таким образом, с учетом вида платежной функции (3), имеем

.

А в силу того, что процесс относительно меры является пуассоновским с интенсивностью имеем

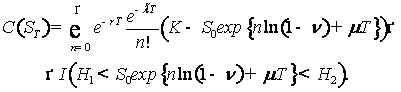(4)

Обозначим

,

.

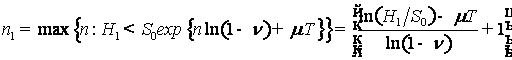Тогда из равенства (4) следует утверждение теоремы.

Литература:

1. Буренин А.Н. Форварды, фьючерсы, опционы, экзотические и погодные производные / А.Н. Буренин. М.: Научно-техническое общество имени академика С.И. Вавилова. –2005. – 534 с.

2.Мельников А.В. Математика финансовых обязательств / А.В. Мельников, М.Л. Нечаев, С.В Волков. –М.: ГУВШЭ. – 2001. – 253 с.

3. Ширяев А.Н. Основы стохастической финансовой математики / А.Н. Ширяев. Т.1. факты и модели. М.: ФАЗИС, 1998. – 512 с.