В.І. Іванов, В.Ю. Зінченко, О.І. Чепрасов, Ю.В. Мосейко
ДЕЯКІ АСПЕКТИ
ПЕРЕНЕСЕННЯ ТЕПЛОТИ ТА МАСИ
ДИФУЗІЄЮ У ТЕРМОДИНАМІЧНИХ СИСТЕМАХ
(Повідомлення 2)
Запорізька державна інженерна академія
Розглядають
перенесення теплової енергії дифузією у закритій термодинамічній системі, що
обмінюється тепловою енергією із довкіллям. Зазначена система є твердим тілом,
тому змінюванням її об’єму 
можна нехтувати.
Тоді рівняння
перенесення теплоти у субстанційній інтерпретації набуває вигляду [1,2]:
.
(1)
Рівняння (1) можна переписати як
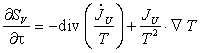. (2)
Виходячи з
теореми про вироблення ентропії, можна записати
. (3)
де 
– швидкість вироблення
ентропії усередині системи за рахунок дисипативних ефектів безповоротних
процесів перенесення теплової енергії; 
– питомий тепловий
потік дифузійного перенесення теплової енергії, що спричинено дією термодинамічної
рушійної сили 
На підставі
принципу лінійності потік внутрішньої енергії у системі, що розглядають,
визначається співвідношенням
,
(4)
де 
– кінетичний
коефіцієнт перенесення внутрішньої енергії.
Вводячи
позначення 
, та використовуючи відоме рівняння
(5)
записують:
. (6)
Оскільки
ентальпія 
, то за 
і рівняння (6) має
вигляд:
,
(7)
де 
, 
– питома масова
теплоємність системи.
За 
та 
мають
.
(8)
Для системи, що складається з двох компонентів, потенціал
перенесення маси одного із них визначають різницею хімічних потенціалів
перенесення (
), тобто відносною величиною енергії, яка є необхідною для
перенесення маси одного компонента із хімічним потенціалом 
до просторової
області, що зайнята іншим компонентом із хімічним потенціалом 
.
Тоді до формули, що подано у роботі [3]
,
(9)
яка визначає дисипативний член, котрий відображає кількісну міру
безповоротності процесу перенесення маси компонентів, вводять відповідні
змінювання:
. (10)
Оскільки згідно з рівнянням Гіббса-Дюгема за 
і 
,
(11)
де 
, 
– відповідно відносні
концентрації першого та другого компонентів системи із середньою щільністю 
, 
; 
, – то градієнт потенціалу перенесення маси складає:
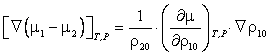. (12)
Маючи це на увазі, записують
. (13)
Тоді
. (14)
Вводять позначення 
та мають
, (15)
Диференційне рівняння масопровідності під час дифузії першого
компонента до просторової області, яка зайнята другим компонентом, набуває вигляду:
. (16)
ПЕРЕЛІК ЛІТЕРАТУРИ
1. Хаазе, Р. Термодинамика
необратимых процессов [Текст] : пер. с нем. ; под ред. А. В. Лыкова.
– М. : Мир, 1967. – 544 с.
2. Кубо, Р. Термодинамика
[Текст] : пер. с англ. ; под ред. Д. Н. Зубарева и Н. М. Плакиды. – М.
: Мир, 1970. – 304 с.
3. Іванов, В. І. Деякі аспекти перенесення теплоти та
маси дифузією у термодинамічних системах [Текст] / В. І. Іванов, В. Ю. Зінченко, О. І Чепрасов,
Ю.В. Мосейко // Modern Scientific Potential-2017. Materials of XIII
International research and practice conference 28.02-07.08.2017.