А.Ш. Кажикенова, Д.Б. Алибиев, А.Б. Сейтимбетова, И.С. Кауымбек

Карагандинский государственный университет им. Е.А. Букетова

Ретсіз бөлшектердің концепциясы негізінде балқымалардың тұтқырлықтарын түсіндіру

Соңғы жылдары түсті және сирек кездесетін жер металдарының нарығындағы бағалар конъюнктурасының өзгеруіне сай, олардың физика-химиялық қасиеттерін, соның ішінде металлургияда тәжірибелік маңызы зор тұтқырлықты зерттеуге қызығушылық артуда. Оған қоса, металл балқымаларының тұтқырлығын зерттеу ғылыми қызығушылық туғызады, өйткені тұтқырлық балқыманың ең құрылымдық-сезімтал сипаттамасының бірі болып табылады.

Сұйық металдық күйді зерттеу кезінде көптеген авторлар алуан түрлі сұйықтық модельдерінің арасында квазикристалды сипаттау концепциясына негізделген модельдерін артықтау санап, соларды ұсынады. Бірақ металдардың балқымаларының құрылымындағы бөлшектердің арасындағы әрекеттесуі мен құрылымын егжей-тегжейлі сипаттауға негізделген тұтқырлықтың белгілі тәуелділіктері мен есептік формулалары температураның шектелген диапазонында ғана орындалады және физикалық мағынасын жоғалтатын екі немесе одан да көп жуықтау параметрлерін қолданады. Түрлі зерттеулердің және түрлі теориялардың есептеулері нәтижесінде алынған тұтқырлық бойынша мәліметтер бірнеше ретке өзгеше болады. Осының барлығы тұтқырлықты түсінудің баламалы тәсілімдемелерінің негізінде қосымша зерттеулерді қажет екендігін көрсетеді.

Ж. Әбішев атындағы Химия-металлургия институтының қызметкерлері техника ғылымдарының докторы, профессор Малышев В.П. және техника ғылымдарының докторы Тұрдықожаева А.М. Больцман үлестірілуіне (теңдеуіне) негізделетін жаңа тәсілдемені ұсынды [1]. Бұл тәсілімдеме ретсіз бөлшектер концепциясы деп аталады. Концепцияға сәйкес заттың үш агрегаттық күйін оның құрылымсыз құрамдас бөлігі бойынша бірыңғай тараптан қарастырады. Барлық жағдайда да ретсіз қозғалыстың энергиясының шамасы бойынша ғана айырмашылығы бар бөлшектер қарастырылады. Ретсіз бөлшектердің концепциясы бойынша кристалды қозғалмалы, сұйықтық қозғалмалы және бу қозғалмалы бөлшектер әрбір заттың агрегатты күйінде де болады.

Бірақ ретсіздіктің түрлі энергетикалық кедергілерін өту және температурасың өсуі барысында осы бөлшектердің үлесі өзгеріп отырады.

Бұл бөлшектердің үлестік қатынасы келесі теңдеуімен есептеледі

Бөлшектердің әр түрін ескере отырып, кинематикалық тұтқырлықтың температуралық тәуелділіктерінің үш моделі ұсынылды:

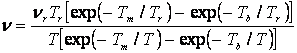
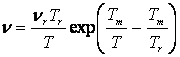
ν_r және T_r – тәжірибе арқылы сенімді анықталған реперлі нүктедегі тұтқырлықтың және температураның мәндері.

Ұсынылған теңдеулерді сұйықтықтың тұтқырлығын сипаттаудың қолданыстағы модельдеріне балама ретінде қарастыруға болады.

Дегенмен, тұтқырлықтың үш моделінің әрқайсысын тексеру қажеттігі және ең дұрыс деген модельді таңдау осындай тәуелділікті құрастырудың әдісінде екіұштылықты туындатады, оған қоса мәліметтерді өңдеуде біршама қиындықтар пайда болады. Бұл жайт ретсіз бөлшектер концепциясының аясында қала отырып, сұйық күйдің табиғатын анағұрлым егжей-тегжейлі қарастыруға себеп болды.

Осы жұмыста біз кластерлердің агрегация дәрежесін ескере отырып, тұтқырлықтың температураға байланысты бірыңғай жалпыланған тәуелділігін ұсынамыз.

Ретсіз бөлшектердің концепциясына сәйкес кластер дегеніміз кристалды қозғалмалы бөлшектерден тұратын түрлі төмен энергиялы комплекстердің өмір сүруінің ықтималды түрі. Біз сұйықтық қозғалмалы және буқозғалмалы бөлшектердің сұйылту қасиетінен басқа температураға байланысты күшті тәуелділігі ассоциацияланған немесе агрегацияланған элементарлы кластерлердің түзілуімен түсіндірілетінін болжаймыз.Сондықтан, (Т_r/Т) фрагментін дәрежеге шығару арқылы он күшейту керектігін ескереміз.

Реперлі нүктені таңдаудың қағидалық мәні болмағанымен, оны кристалдану нүктесінің маңында тіркеген жөн. Бірақ нүктенің өзінде емес, өйткені төмен температурада тұтқырлық сенімдірек анықталады және мәндері үлкен болып келеді.

Бұл жердегі a көрсеткіші кластерлердің ассоциациясының орташа дәрежесі мағынасына ие.

а көрсеткішін есептеу формуласын тұжырымдау үшін (2) теңдеуді математикатикалық түрлендіреміз, яғни логарифмдейміз.

Алынған мәндер жиынының статистикалық біртектілігі Налимов критериі бойынша бағаланады, алынған мәліметтерді тәжірибелік мәліметтермен салыстыру барысында олардың дұрыстығы сызықтық емес жиындық корреляция коэффициенті арқылы және оның маңыздылығы арқылы тексерілді.

Литература

1. Малышев В.П., Турдукожаева А.М., Кажикенова А.Ш. Вязкость расплавов металлов по концепции хаотизированных частиц // Тяжелое машиностроение. – 2009. – № 6. – С. 37-39.