Безвесільна О.М., д.т.н., професор; Ткачук А.Г., к.т.н.;

Коваль А.В., к.т.н.; Шарапов Д.Д., магістрант

Національний технічний університету України «Київський політехнічний інститут ім. Ігоря Сікорського», Україна

Житомирський державний технологічний університет, Україна

ТРИСТУПЕНЕВИЙ ГІРОСКОП ЯК ЧУТЛИВИЙ ЕЛЕМЕНТ СИСТЕМИ СТАБІЛІЗАЦІЇ ОЗБРОЄННЯ

Системи стабілізації різних видів застосовуються у навігаційних пристроях і системах управління кораблів і літальних апаратів, а також у системах орієнтації антен, телескопів та інших приладів, встановлених на рухомих об'єктах. У зв'язку з тим, що необхідна точність подібних пристроїв безперервно підвищується, ростуть і вимоги до точності, що вимагається від комплексів стабілізації. Існуючі системи стабілізації не можуть сьогодні достатньо ефективно виконувати поставлені перед ними завдання. За досвідом воєнних конфліктів, найбільша частина втрат парку броньових машин є наслідком використання малоефективних систем стабілізації озброєння. Тому забезпечення покращення експлуатаційних характеристик комплексу стабілізації озброєння ЛБТ є найважливішою проблемою сучасності, вирішення якої забезпечує навігаційну безпеку України.

Для цілей гіроскопічної стабілізації застосовуються гіроскопи, що являють собою симетричне тверде тіло (ротор), що швидко обертається навколо осі симетрії. Одна з точок тіла на осі обертання закріплена і називається точкою підвісу. У разі збігу точки підвісу з центром тяжіння виходить так званий астатичний гіроскоп. Сьогодні відомо багато різновидів гіроскопів. Відмінність між ними полягає у способі підвісу ротора. Відповідно до цього, розрізняють гіроскопи з шарикопідшипниковими опорами, поплавкові, з аеродинамічним підвісом, з магнітним підвісом і т.д.

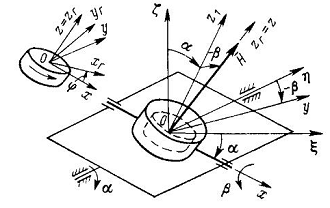
Якщо помістити кожух з ходовими підшипниками в двовісний карданний підвіс (рис. 1), то вийде триступеневий гіроскоп. Положення гіроскопа відносно нерухомого об'єкта, на якому встановлений підвіс, може бути визначено шляхом порівняння положення координатної системи , пов'язаної з обертовим ротором, з нерухомою системою координат Перехід від однієї системи координат до іншої може бути зроблений поворотом на три кути Ейлера.

Рис.1. Гіроскоп у кардановому підвісі

Перший поворот на кут прецесії здійснюється навколо осі зовнішньої рамки (осі ), другий поворот на кут нутації - щодо осі внутрішньої рамки (осі ) і третій поворот на кут власного обертання гіроскопа - щодо осі обертання ротора (осі ). Зауважимо, що в гіроскопічних стабілізаторах кут , зазвичай, називається кутом стабілізації, а кут - кутом прецесії.

Рівняння руху гіроскопа, як правило, виводять для напіврухомої системи координат (тригранника Резаля), у якій вісь збігається з віссю власного обертання гіроскопа, а осі і пов'язані з внутрішнім кільцем підвісу, тобто з кожухом гіроскопа (рис. 1). У цій системі координат вихідні рівняння руху гіроскопа мають вигляд:

	(1)
	(2)
	(3)

де , и - проекції вектора абсолютної кутової швидкості обертання напіврухомої системи координат у просторі на осі напіврухомої системи координат; , і - відповідні моменти ітерації; , і - моменти зовнішніх сил; - кінетичний момент.

Рівняння (1) і (2) описують рух осі гіроскопа. Ці рівняння зручніше представити так, щоб в них входили моменти, що діють по осях підвісу. Крім того, будемо нехтувати в рівняннях (1) і (2) впливом членів, що містять швидкості. Тоді, враховуючи очевидні рівності і , отримаємо після проектування на відповідні осі:

	(4)
	(5)

У цих рівняннях і - кути повороту щодо осей зовнішньої і внутрішньої рамок; - момент інерції системи відносно осі зовнішньої рамки (осі ) і - момент інерції внутрішньої рамки (кожуха з гіроскопом) щодо її осі (осі ). При малих значеннях кута можна прийняти . Переходячи до символічного запису диференційних рівнянь і вводячи алгебраїчний оператор диференціювання , отримаємо лінеаризовані рівняння:

	(6)
	(7)

У ці рівняння входять не самі оригінали функцій и , а їх зображення. Рівняння (6) і (7) можна прив’язати до кутів повороту підвісу:

	(8)
	(9)

де - квадрат кругової частоти нутаційних коливань гіроскопа.

Література:

1. Безвесільна О. М. Системи керування навігаційних систем рухомих об'єктів: Монографія / О. М. Безвесільна, Ю.В. Киричук, С.С. Ткаченко – Житомир, ЖДТУ, 2010. - 174с.

2. Безвесільна О.М., Квасніков В.П., Цірук В.Г., Чіковані В.В. Системи наведення та стабілізації озброєння. - Житомир: ЖДТУ, 2014. – 176 с.

3. Безвесільна О.М. Алгоритмічний метод підвищення точності вимірювачів лінійних прискорень стабілізатора / О.М. Безвесільна, А.Г. Ткачук, О.В. Кравцов, М.П. Туленко // Вісник інженерної академії наук України. - 2016. – №2. – С. 58-63.

4. Безвесільна О.М. Розрахунок та аналіз статичних похибок двогіроскопного чутливого елемента / О.М. Безвесільна, А.Г. Ткачук, А.А.Гуменюк, С.О. Нечай // Науковий журнал «Технологічний аудит та резерви виробництва». – 2016. – № 6/2(32). – С. 9-17.

5. Безвесільна О. М. Технологічні вимірювання та прилади. Перетворюючі пристрої приладів: Підручник / О. М. Безвесільна, Г.С. Тимчик – Житомир, ЖДТУ, 2012. - 812 с.

6. Безвесільна О.М., Маляров С.П., Цірук В.Г., Чепюк Л.О. Оптимізація, ідентифікація, алгоритмічна обробка параметрів чутливих елементів стабілізатора легкої броньованої техніки: Монографія - Житомир: ЖДТУ, 2015. – 217 с.

7. Безвесільна О.М. Розрахунок пружного модуля системи ударо- і віброзахисту стабілізатора озброєння легкої броньованої техніки / О.М. Безвесільна, А.Г. Ткачук, Ю.В. Киричук // Вісник інженерної академії наук України. – 2016. – №2. – С. 51-57.

8. Патент на винахід №109746 від 25.09.2015р. Бюл. №18 по заявці на винахід № а 2014 08137 від 18.07.2014 бюл. №1 від 12.01.2015Авіаційна гравіметрична система для вимірювань аномалій прискорення сили тяжіння Ткачук А.Г., Чепюк Л.А.