Технические науки/ 4.Транспорт

Д.т.н., проф. Кадыров А.С., докторант Кызылбаева Э.Ж.

Карагандинский Государственный Технический университет, РК

Установление оптимального времени

начала складирования узлов, агрегатов по критерию

минимума ущерба

Для оценки надежности и эффективности технической эксплуатации автомобильного подвижного состава, в том числе и эксплуатируемого на горных предприятиях, используется целый ряд показателей, как предусмотренных ГОСТ 27.002-89 ≪Надежность в технике. Термины и определения≫, так и не предусмотренных этим стандартом.

Это обусловлено, прежде всего, тем, что анализом показателей надежности автотранспорта занимаются конструкторы, изготовители, службы технической и производственной эксплуатации, которые интересуются различными аспектами работоспособности машин. Кроме того, в транспортной автомобильной отрасли исторически сложилась своя система понятий и показателей эксплуатационно-технологических свойств автомобильного подвижного состава. В формирование этой системы внесли свой вклад и ученые-горняки.

Наиболее крупными работами по надежности и техническому обслуживанию автотранспорта общего назначения являются работы проф. Е.С. Кузнецова [1]. Вопросы надежности узлов и агрегатов карьерных автосамосвалов, а также машин в сборе наиболее полно отражены в работах З.Л. Сироткина, А.Н. Казареза, А.Н. Егорова, А.А. Кулешова, П.И. Тарасова и др. Вопросы надежности карьерного транспортного комплекса в целом рассмотрены в трудах М.В. Васильева, А.А. Кулешова [2], В.Л. Яковлева, М.Г. Потапова и др.

Для оценки надежности отдельных узлов и агрегатов карьерных автосамосвалов используется основная стандартизованная величина — вероятность безотказной работы F(t) в зависимости от времени работы t (или от пробега L).

Длительность времени безотказной работы узла детали имеет показательное распределение вида:

(1)

где t – время безотказной работы;

λ – интенсивность отказов.

Закон надежности (исходя из 1) имеет вид:

(2)

В случае, если детали нет на складе имеем ущерб от простоя без ремонта и т.т. U_x

где ν – вероятность детали на складе

t₁ – время ожидания детали и ремонта

U_ч – чистый ущерб

Считая, что вероятность определятся законом (1) получим

(3)

С другой стороны, если деталь есть на складе, и не используется, ущерб от складирования составит

(4)

С – стоимость детали с затратами на хранение;

t_xp. – время хранения;

U_xp. – затраты на хранение.

Начинать хранение детали выгодно с момента, когда U_x=U_c, т.к. до этого времени капиталы омертвляются, и после него возникает риск увеличения U_x (рисунок 1).

Имеем U_x=U_c ,

Откуда

(5)

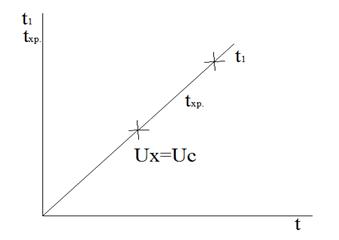
Рисунок 1 – U_x = U_c

Величина отклонения

Пример: Считаем, что за период 1000часов количество отказов детали составило 10раз. Интенсивность составила λ=10/1000=0,01. Согласно закона надежности (2) найдем вероятность безотказной работы детали в течении 100 часов:

.

Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивности отказов).

Литература:

1. Кузнецов Е.С. Техническое обслуживание и надежность автомобилей. —

М.: Транспорт, 1972.-224 с.

2. Казарез А.Н., Кулешов A.A., Резников С.Н. Определение производительности карьерного автотранспорта.- Промышленный транспорт, 1986, № 8.